题目内容
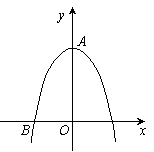
如图11,抛物线y=ax2 + c经过点A(0,2)和点B( -1,0).
-1,0).
(1)求此抛物线的解析式;
(2)将此抛物线平移,使其顶点坐标为(2,1),平移后的抛物线与x轴的两个交点分别为点C,D(点C在点D的左边),求点C,D的坐标;
(3)将此抛物线平移,设其顶点的纵坐标为m,平移后的抛物线与x轴两个交点之间的距离为n,若1<m<3,直接写出n的取 值范围.
值范围.
 |
解:(1)∵抛物线y=ax2 + c经过点A(0,2)和点B(-1,0);
∴ 
解得: 
∴此抛物线的解析式为
(2)∵此抛物线平移后顶点坐标为(2,1)
∴抛物线的解析式为y=-2 +1
+1
令y=0, 即-2 +1=0
+1=0
解得 

∵点C在点D的左边
∴C( ,0) D(
,0) D( ,0)
,0) 
(3) <n<
<n<

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中自变量x的取值范围是 .
中自变量x的取值范围是 .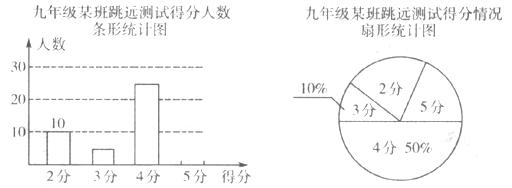
 B.
B. C.2 D.
C.2 D.

 .北偏西60°
.北偏西60°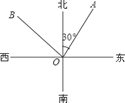
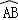 的长为( )
的长为( )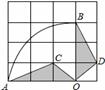

 的值不
的值不 小于-4且小于8.
小于-4且小于8.