题目内容
 已知,如图,AD为△ABC的内角平分线,且AD=AB,CM⊥AD于M.求证:AM=
已知,如图,AD为△ABC的内角平分线,且AD=AB,CM⊥AD于M.求证:AM= (AB+AC).
(AB+AC).
证明:延长AM到点E,使得:ME=MD,连接CE.
∵CM是DE的垂直平分线,
∴CD=CE,
∵AB=AD,
∴∠E=∠CDE=∠ADB=∠B,
∵∠ACE=180°-∠CAE-∠E=180°-∠BAD-∠ADB=∠B=∠E,
∴AC=AE,
AM= (AM+AM)
(AM+AM)
= (AM-MD+ME+AM)
(AM-MD+ME+AM)
= (AD+AE)
(AD+AE)
= (AB+AC),
(AB+AC),
即AM= (AB+AC).
(AB+AC).
分析:延长AM到点E,使得:ME=MD,连接CE,根据等角对等边得出∠E=∠CDE=∠ADB=∠B,求出∠ACE=∠B=∠E,推出AC=AE,代入AM= (AM+AM)即可求出答案.
(AM+AM)即可求出答案.
点评:本题主要考查对等腰三角形的性质和判定,三角形的内角和定理,对顶角相等等知识点的理解和掌握,能推出AC=AE是解此题的关键.

∵CM是DE的垂直平分线,
∴CD=CE,
∵AB=AD,
∴∠E=∠CDE=∠ADB=∠B,
∵∠ACE=180°-∠CAE-∠E=180°-∠BAD-∠ADB=∠B=∠E,
∴AC=AE,
AM=
 (AM+AM)
(AM+AM)=
 (AM-MD+ME+AM)
(AM-MD+ME+AM) =
 (AD+AE)
(AD+AE) =
 (AB+AC),
(AB+AC),即AM=
 (AB+AC).
(AB+AC).分析:延长AM到点E,使得:ME=MD,连接CE,根据等角对等边得出∠E=∠CDE=∠ADB=∠B,求出∠ACE=∠B=∠E,推出AC=AE,代入AM=
 (AM+AM)即可求出答案.
(AM+AM)即可求出答案.点评:本题主要考查对等腰三角形的性质和判定,三角形的内角和定理,对顶角相等等知识点的理解和掌握,能推出AC=AE是解此题的关键.

练习册系列答案
相关题目
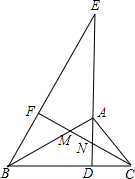 已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
 已知,如图,AD为△ABC的内角平分线,且AD=AB,CM⊥AD于M.求证:AM=
已知,如图,AD为△ABC的内角平分线,且AD=AB,CM⊥AD于M.求证:AM= 已知,如图:AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.求证:AB=CE.
已知,如图:AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.求证:AB=CE. (AB+AC)
。
(AB+AC)
。