题目内容
19.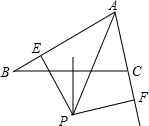 已知:如图,∠BAC的平分线与BC的垂直平分线相交于点P,PE⊥AB,PF⊥AC,垂足分别为E、F.若AB=8,AC=4,则AE=6.
已知:如图,∠BAC的平分线与BC的垂直平分线相交于点P,PE⊥AB,PF⊥AC,垂足分别为E、F.若AB=8,AC=4,则AE=6.
分析 首先连接PB,PC,由∠BAC的平分线与BC的垂直平分线相交于点P,PE⊥AB,PF⊥AC,易得PE=PF,PB=PC,继而证得△PBE≌△PCF,AE=AF,又由AB=8,AC=4,即可求得答案.
解答 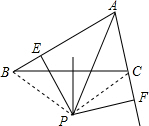 解:连接PB,PC,
解:连接PB,PC,
∵点P在BC的垂直平分线上,
∴PB=PC,
∵AC平分∠BAC,PE⊥AB,PF⊥AC,
∴PE=PF,∠PEB=∠PFC=90°,
∴∠APE=∠APF,
∴AE=AF,
在Rt△PBE和Rt△PCF中,
$\left\{\begin{array}{l}{PB=PC}\\{PE=PF}\end{array}\right.$,
∴Rt△PBE≌Rt△PCF(HL),
∴BE=CF,
∵AB=AE+BE,AF=AC+CF,
∴AB=AC+CF+BE,
∵AB=8,AC=4,
∴BE=CF=2,
∴AE=AC+CF=6.
故答案为:6.
点评 此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
9.下列各式中,合并同类项正确的是( )
| A. | 6a-5a=1 | B. | 2a+3b=5ab | C. | 4x2y-5y2x=-x2y | D. | 13xy-13yx=0 |
 如图,已知正方形ABCD,AB=8,AD=4,E为CD边上一点,CE=5.
如图,已知正方形ABCD,AB=8,AD=4,E为CD边上一点,CE=5.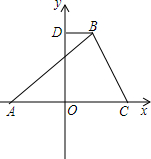 如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4$\sqrt{5}$,∠BAC=45°.
如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4$\sqrt{5}$,∠BAC=45°. 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.