题目内容
11.解方程(1)(x-2)2=1
(2)3x2-6x+1=0
(3)x(x+2)=6x+12
(4)x2-2x-54=0.
分析 (1)直接开平方即可;
(2)用公式法求解即可;
(3)先提公因式,再移项,再提公因式即可得出关于x的两个一元一次方程;
(4)先移项,再配方,即可得出方程的解.
解答 解:(1)x-2=±1,
x-2=1或x-2=-1,
x1=3,x2=1;
(2)a=3,b=-6,c=1,
x=$\frac{6±\sqrt{36-12}}{6}$,
x=$\frac{6±2\sqrt{6}}{6}$,
x1=$\frac{3+\sqrt{6}}{3}$,x2=$\frac{3-\sqrt{6}}{3}$;
(3)x(x+2)=6(x+2),
(x-6)(x+2)=0,
x-6=0或x+2=0,
x1=6,x2=-2;
(4)(x-1)2=55,
x-1=±$\sqrt{55}$,
x-1=$\sqrt{55}$或x-1=-$\sqrt{55}$
x1=1+$\sqrt{55}$,x2=1-$\sqrt{55}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
1.下列说法不正确的是( )
| A. | 0的平方根是0 | B. | 一个正数的立方根是一个正数 | ||
| C. | 8的算术平方根是4 | D. | -8的立方根是-2 |
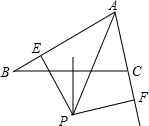 已知:如图,∠BAC的平分线与BC的垂直平分线相交于点P,PE⊥AB,PF⊥AC,垂足分别为E、F.若AB=8,AC=4,则AE=6.
已知:如图,∠BAC的平分线与BC的垂直平分线相交于点P,PE⊥AB,PF⊥AC,垂足分别为E、F.若AB=8,AC=4,则AE=6. 如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E
如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E