题目内容
 已知:如图BE∥CF,BE、CF分别平分∠ABC和∠BCD,求证:AB∥CD
已知:如图BE∥CF,BE、CF分别平分∠ABC和∠BCD,求证:AB∥CD
证明:∵BE、CF分别平分∠ABC和∠BCD(已知)
∴∠1= ∠________∠2=
∠________∠2= ∠________(________)
∠________(________)
∵BE∥CF(________)
∴∠1=∠2(________)
∴ ∠ABC=
∠ABC= ∠BCD
∠BCD
即∠ABC=∠BCD
∴AB∥CD(________)
ABC BCD 角平分线的定义 已知 两直线平行,内错角相等 内错角相等,两直线平行
分析:先利用角平分线的定义填空,再根据平行线的性质和判定填空.
解答:∵BE、CF分别平分∠ABC和∠BCD(已知),
∴∠1= ∠ABC,∠2=
∠ABC,∠2= ∠BCD(角平分线的定义);
∠BCD(角平分线的定义);
∵BE∥CF(已知),
∴∠1=∠2(两直线平行,内错角相等),
∴ ∠ABC=
∠ABC= ∠BCD,
∠BCD,
即∠ABC=∠BCD,
∴AB∥CD(内错角相等,两直线平行).
点评:本题主要考查证明过程中理论依据的填写,训练学生证明步骤的书写,比较简单.
分析:先利用角平分线的定义填空,再根据平行线的性质和判定填空.
解答:∵BE、CF分别平分∠ABC和∠BCD(已知),
∴∠1=
 ∠ABC,∠2=
∠ABC,∠2= ∠BCD(角平分线的定义);
∠BCD(角平分线的定义);∵BE∥CF(已知),
∴∠1=∠2(两直线平行,内错角相等),
∴
 ∠ABC=
∠ABC= ∠BCD,
∠BCD,即∠ABC=∠BCD,
∴AB∥CD(内错角相等,两直线平行).
点评:本题主要考查证明过程中理论依据的填写,训练学生证明步骤的书写,比较简单.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
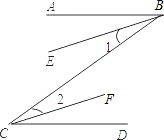 已知:如图BE∥CF,BE、CF分别平分∠ABC和∠BCD,求证:AB∥CD
已知:如图BE∥CF,BE、CF分别平分∠ABC和∠BCD,求证:AB∥CD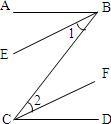


 ∠ ∠2=
∠ ∠2=
 ∠ ∠2=
∠ ∠2=
 ∠( ),( )
∠( ),( )