题目内容
4．如图，下列平面图形经过折叠后可以围成一个长方体的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据长方形展开图的特点或者固定一个面其他的面合围判断是否构成封闭的长方体．
解答 解：A、缺少一个面，不能围成长方体；
B、缺少一个面，不能围成长方体；
C、固定最下方中间的矩形做底面，上方3个矩形依次围过来分别构成长方体的后、上、前三面，
左右两个正方形围起来构成长方体的左右侧面，可以围成一个长方体；
D、右边两个小正方形围到一起后重叠，不能围成一个长方体；
故选：C．
点评 本题考查长方体展开图的特征，长方体展开图的四个侧面是完全相同的矩形，上下底面展开后是两个相同的矩形也有可能是正方形．
练习册系列答案
相关题目
14．已知等边△ABC的一边长为10，则它的周长是（ ）
| A． | 10 | B． | 20 | C． | 30 | D． | 40 |
15．十八世纪瑞士数学家欧拉证明了简单多面体的顶点数（V）、面树（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：
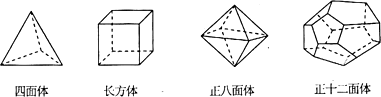
（1）根据上面多面体模型，填写表格中的空格：
（2）根据上面的表格，猜想顶点数（V）、面数（F）、棱数（E）之间存在的关系式是V+F-E=2（用所给的字母表达）；
（2）若一个多面体的面数比顶点数少14，且有48条棱，则这个多面体的面数是18；
（3）有一个玻璃饰品的外形是简单多面体，它共有24个顶点，每个顶点处都有3条棱，设该多面体的面数为x，求x的值．
（1）根据上面多面体模型，填写表格中的空格：
| 多面体 | 顶点数（V） | 面数（F） | 棱数（E） |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
（2）若一个多面体的面数比顶点数少14，且有48条棱，则这个多面体的面数是18；
（3）有一个玻璃饰品的外形是简单多面体，它共有24个顶点，每个顶点处都有3条棱，设该多面体的面数为x，求x的值．
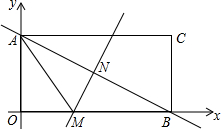如图，长方形AOBC在直角坐标系中，点A在y轴上，点B在x轴上，已知点C的坐标是（8，4）．
13．
如图，△ABC是等边三角形，CB=BD，连接AD，∠ACD=110°，则∠BAD的度数为（ ）
如图，△ABC是等边三角形，CB=BD，连接AD，∠ACD=110°，则∠BAD的度数为（ ）| A． | 10° | B． | 15° | C． | 20° | D． | 25° |