题目内容
已知四边形ABCD和四边形A1B1C1D1相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,如果四边形A1B1C1D1的最短边的长是6cm,那么四边形A1B1C1D1中最长的边长是 cm.
考点:相似多边形的性质
专题:
分析:利用相似多边形的性质得出相似比,进而求出即可.
解答:解:∵四边形ABCD和四边形A1B1C1D1相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,
四边形A1B1C1D1的最短边的长是6cm,
∴两多边形的相似比为:
=
,
那么四边形A1B1C1D1中最长的边长是:10÷
=15(cm).
故答案为:15.
四边形A1B1C1D1的最短边的长是6cm,
∴两多边形的相似比为:
| 4 |
| 6 |
| 2 |
| 3 |
那么四边形A1B1C1D1中最长的边长是:10÷
| 2 |
| 3 |
故答案为:15.
点评:此题主要考查了相似多边形的性质,得出相似比是解题关键.

练习册系列答案
相关题目
若实数a≠b,且a,b满足a2-8a+5=0,b2-8b+5=0,则代数式
+
的值为( )
| b-1 |
| a-1 |
| a-1 |
| b-1 |
| A、-20 | B、2 |
| C、2或-20 | D、2或20 |
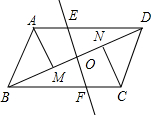 如图,?ABCD中,O是对角线BD中点,过点O的直线和AD、BC分别相交于E、F,AM平分∠BAD,CN平分∠DCB.请在平行四边形ABCD的基础上添加适当的条件,构造新的平行四边形,进而谈谈你的感想.
如图,?ABCD中,O是对角线BD中点,过点O的直线和AD、BC分别相交于E、F,AM平分∠BAD,CN平分∠DCB.请在平行四边形ABCD的基础上添加适当的条件,构造新的平行四边形,进而谈谈你的感想.