题目内容
20.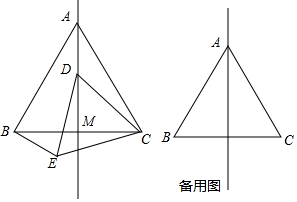 各边相等且各个内角相等的三角形称为等边三角形.如图,在等边△ABC中,线段AM为BC边上的高.动点D在射线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
各边相等且各个内角相等的三角形称为等边三角形.如图,在等边△ABC中,线段AM为BC边上的高.动点D在射线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.(1)填空:∠ACB=60度;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动点D在射线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
分析 (1)根据等边三角形的性质:等边三角形的每一个内角都等于60°进行解答;
(2)根据等边三角形的性质就可以得出AC=AC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;
(3)分情况讨论:当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,就可以求出结论;当点D在线段AM的延长线上时,如图2,可以得出△ACD≌△BCE,进而得到∠CBE=∠CAD=30°,据此得出结论.
解答 解:(1)∵△ABC是等边三角形,
∴∠ACB=60°;
故答案为:60;
(2)∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE.
在△ADC和△BEC中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS);
(3)∠AOB是定值,∠AOB=60°,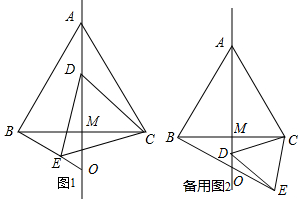
理由如下:∵AD为等边三角形的高,
∴∠AMC=∠AMB=90°,∠CAO=$\frac{1}{2}$∠BAC=30°,∠ACB=60°,
①当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,则
∠ABE=∠CAD=30°,
又∵∠AMC=∠BMO,
∴∠AOB=∠ACB=60°
②当点D在线段AM的延长线上时,如图2,
∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠DCB=∠DCB+∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠CBE=∠CAD=30°,
又∵∠AMC=∠BMO,
∴∠AOB=∠ACB=60°.
综上所述,当动点D在射线AM上时,∠AOB为定值60°.
点评 本题考查了等边三角形的性质的运用,直角三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.解题时注意:全等三角形的对应角相等;等边三角形的三个内角都相等,且都等于60°.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案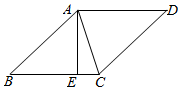 如图,在菱形ABCD中,AB=13,对角线AC=10,若过点A作AE⊥BC,垂足为E,则AE的长为( )
如图,在菱形ABCD中,AB=13,对角线AC=10,若过点A作AE⊥BC,垂足为E,则AE的长为( )| A. | 8 | B. | $\frac{60}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{240}{13}$ |
| A. | ±3 | B. | -3 | C. | 3 | D. | ±$\sqrt{3}$ |
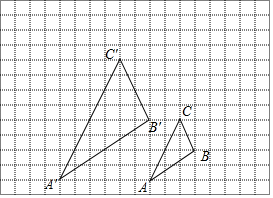 如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形顶点上.
如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形顶点上.(1)画出位似中心点O;
(2)△ABC与△A′B′C′的位似比为1:2.
| A. | x2 | B. | |-x-1| | C. | -x2+1 | D. | |x+y|+1 |
| A. | (x+2)(x-2)=x2-4 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2+4=(x+2)2 |
 如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.
如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.