题目内容
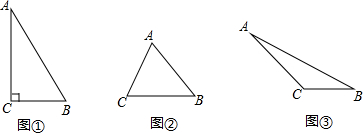
在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)试证明(2)中猜想的正确性.
(1)当△ABC三边分别为6、8、9时,△ABC为
(2)猜想,当a2+b2
(3)试证明(2)中猜想的正确性.

考点:勾股定理的逆定理
专题:
分析:(1)利用勾股定理列式求出两直角边为6、8时的斜边的值,然后作出判断即可;
(2)根据(1)中的计算作出判断即可;
(3)若△ABC是锐角三角形,则有a2+b2>c2;理由:过点A作AD⊥BC,垂足为D,设CD为x,则有BD=a-x.根据勾股定理,得a2+b2=c2+2ax,从而可证;
当△ABC是钝角三角形时,a2+b2<c2;理由:过B作BD⊥AC,交AC的延长线于D.设CD为x,则有BD2=a2-x2,根据勾股定理,得a2+b2+2bx=c2,从而可证.
(2)根据(1)中的计算作出判断即可;
(3)若△ABC是锐角三角形,则有a2+b2>c2;理由:过点A作AD⊥BC,垂足为D,设CD为x,则有BD=a-x.根据勾股定理,得a2+b2=c2+2ax,从而可证;
当△ABC是钝角三角形时,a2+b2<c2;理由:过B作BD⊥AC,交AC的延长线于D.设CD为x,则有BD2=a2-x2,根据勾股定理,得a2+b2+2bx=c2,从而可证.
解答:解:(1)∵两直角边分别为6、8时,斜边=
=10,
∴△ABC三边分别为6、8、9时,△ABC为锐角三角形;
当△ABC三边分别为6、8、11时,△ABC为钝角三角形;
故答案为:锐角;钝角;
(2)当a2+b2>c2时,△ABC为锐角三角形;
当a2+b2<c2时,△ABC为钝角三角形;
故答案为:>;<;
(3)若△ABC是锐角三角形,则有a2+b2>c2;
理由:过点A作AD⊥BC,垂足为D,设CD为x,
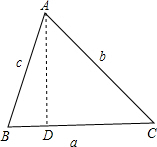
则有BD=a-x.
根据勾股定理,得b2-x2=AD2=c2-(a-x)2,
即b2-x2=c2-a2+2ax-x2.
则a2+b2=c2+2ax.
∵a>0,x>0,
∴2ax>0;
∴a2+b2>c2.
当△ABC是钝角三角形时,a2+b2<c2;
理由:过B作BD⊥AC,交AC的延长线于D.
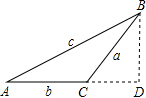
设CD为x,则有BD2=a2-x2,
根据勾股定理,得(b+x)2+a2-x2=c2,即a2+b2+2bx=c2.
∵b>0,x>0,
∴2bx>0,
∴a2+b2<c2.
| 62+82 |
∴△ABC三边分别为6、8、9时,△ABC为锐角三角形;
当△ABC三边分别为6、8、11时,△ABC为钝角三角形;
故答案为:锐角;钝角;
(2)当a2+b2>c2时,△ABC为锐角三角形;
当a2+b2<c2时,△ABC为钝角三角形;
故答案为:>;<;
(3)若△ABC是锐角三角形,则有a2+b2>c2;
理由:过点A作AD⊥BC,垂足为D,设CD为x,

则有BD=a-x.
根据勾股定理,得b2-x2=AD2=c2-(a-x)2,
即b2-x2=c2-a2+2ax-x2.
则a2+b2=c2+2ax.
∵a>0,x>0,
∴2ax>0;
∴a2+b2>c2.
当△ABC是钝角三角形时,a2+b2<c2;
理由:过B作BD⊥AC,交AC的延长线于D.

设CD为x,则有BD2=a2-x2,
根据勾股定理,得(b+x)2+a2-x2=c2,即a2+b2+2bx=c2.
∵b>0,x>0,
∴2bx>0,
∴a2+b2<c2.
点评:本题考查了勾股定理,勾股定理逆定理,读懂题目信息,理解三角形为锐角三角形、直角三角形、钝角三角形时的三条边的数量关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列概念表述正确的是( )
| A、单项式ab的系数是0,次数是2 | ||
| B、-2πx2y3的系数是-2,次数是6 | ||
C、
| ||
| D、-ab2+3a-1的项是-ab2、3a、1 |