题目内容
3.已知:在△ABC中,三边长分别为a、b、c,化简|a+b-c|-|b-a+c|+|b-a-c|.分析 根据三角形的任意两边之和大于第三边可得a+b-c>0,b-a+c>0,b-a-c<0,再根据绝对值的性质去掉绝对值符号,然后利用整式的加减运算进行计算即可得解
解答 解:∵a、b、c分别为△ABC的三边长,
∴a+b-c>0,b-a+c>0,b-a-c<0,
∴|a+b-c|-|b-a+c|+|b-a-c|
=a+b-c-b+a-c-b+a+c
=3a-b-c.
点评 本题考查了三角形的三边关系,绝对值的性质,整式的加减运算,熟记性质并去掉绝对值符号是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
13.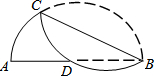 将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )
将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )
 将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )
将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )| A. | 6$\sqrt{7}$ | B. | 16 | C. | 2$\sqrt{65}$ | D. | 4$\sqrt{15}$ |
8.如果将向东行驶3km记作+3km,那么向西行驶2km应记作( )
| A. | +2km | B. | -2km | C. | +3km | D. | -3km |
 观察如图规律,则A等于40.
观察如图规律,则A等于40.