题目内容
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.则当收绳8秒后船向岸边移动了 米(结果保留根号).

考点:
勾股定理的应用..
分析:
根据直角三角形30°角所对的直角边等于斜边的一半求出BC,再根据勾股定理列式求出AB,然后求出收绳8秒后船的位置B′距点C的长度,再根据勾股定理列式求出AB′的长度,然后列式计算即可得到船移动的距离.
解答:
解:如图,∵AC=5米,∠B=30°,AC⊥AB,
∴BC=2AC=2×5=10米,
根据勾股定理,AB=![]() =
=![]() =5
=5![]() 米,
米,
收绳8秒后,设船的位置为B′,
∵0.5×8=4米,
∴B′C=10﹣4=6米,
根据勾股定理,AB′=![]() =
=![]() =
=![]() ,
,
故BB′=AB﹣AB′=(5![]() ﹣
﹣![]() )米.
)米.
故答案为:(5![]() ﹣
﹣![]() ).
).

点评:
本题考查了勾股定理的应用,难点不大,读懂题目信息求出8秒后船的位置与点C的长度是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
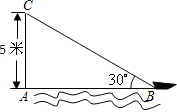 如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:8秒后船向岸边移动了多少米?(结果精确到0.1米)
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:8秒后船向岸边移动了多少米?(结果精确到0.1米)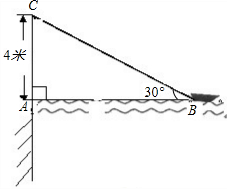 角为30°.
角为30°. 如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:未开始收绳子的时候,图中绳子BC的长度是
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:未开始收绳子的时候,图中绳子BC的长度是 如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.则当收绳8秒后船向岸边移动了
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.则当收绳8秒后船向岸边移动了