题目内容
 如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:未开始收绳子的时候,图中绳子BC的长度是
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:未开始收绳子的时候,图中绳子BC的长度是分析:利用30°的正弦值可得未开始收绳子的时候,图中绳子BC的长度;
利用30°的余弦值可得未开始收绳子的时候AB长,易得收绳后BC长,利用勾股定理可得收绳后AB长,让未收绳时AB长减去收绳后AB长即为船向岸边移动的距离.
利用30°的余弦值可得未开始收绳子的时候AB长,易得收绳后BC长,利用勾股定理可得收绳后AB长,让未收绳时AB长减去收绳后AB长即为船向岸边移动的距离.
解答: 解:(1)如图,在Rt△ABC中,
解:(1)如图,在Rt△ABC中,
=sin30°,
∴BC=
=10米;
(2)未收绳时AB=5÷tan30°=5
米
收绳8秒后,绳子BC缩短了4米,只有6米,即CD=6米,
在Rt△ACD中,由AC=5米,CD=6米,
根据勾股定理得船到河岸的距离AD=
=
=
米.
故移动距离DB=AB-AD=(5
-
)米,
故答案为(5
-
).
 解:(1)如图,在Rt△ABC中,
解:(1)如图,在Rt△ABC中,| AC |
| BC |
∴BC=
| 5 |
| sin30° |
(2)未收绳时AB=5÷tan30°=5
| 3 |
收绳8秒后,绳子BC缩短了4米,只有6米,即CD=6米,
在Rt△ACD中,由AC=5米,CD=6米,
根据勾股定理得船到河岸的距离AD=
| 62-52 |
| 36-25 |
| 11 |
故移动距离DB=AB-AD=(5
| 3 |
| 11 |
故答案为(5
| 3 |
| 11 |
点评:考查解直角三角形在实际生活中的应用,用到的知识点为:知道对边求斜边,可用正弦值,用除法;知道对边,求邻边,用除法,用正切值.

练习册系列答案
相关题目
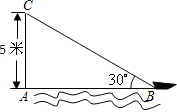 如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:8秒后船向岸边移动了多少米?(结果精确到0.1米)
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:8秒后船向岸边移动了多少米?(结果精确到0.1米)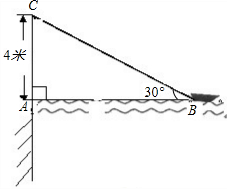 角为30°.
角为30°. 如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.则当收绳8秒后船向岸边移动了
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.则当收绳8秒后船向岸边移动了