题目内容
如图，设正方体ABCD-A1B1C1D1的棱长为1m，黑、白两虫同时从A点出发，黑虫以1m/分钟、白虫以0.5m/分钟的速度分别沿棱向前爬行，黑虫爬行路线是AA1→A1D1→…，白虫爬行路线是AB→BB1→…，且都遵循如下规则：所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交（其中n是正整数）．那么当黑、白两虫爬行完2014分钟时，它们之间的距离是（ ）A、
| ||
| B、0 | ||
C、
| ||
| D、1 |
考点：规律型：图形的变化类
专题：
分析：先确定黑、白两个虫各爬行完第2014条棱分别停止的点，再根据勾股定理求出它们之间的位置．
解答：
解：连接CD1，
因为2014÷6=335…4，所以黑、白两个甲壳虫各爬行完第2014条棱分别停止的点是C和D1，
由于∠CDD1=90°，
所以根据勾股定理：CD1=
=
．
故选A．
解：连接CD1，因为2014÷6=335…4，所以黑、白两个甲壳虫各爬行完第2014条棱分别停止的点是C和D1，
由于∠CDD1=90°，
所以根据勾股定理：CD1=
| 12+12 |
| 2 |
故选A．
点评：此题是一道趣味性题目，不仅考查了阅读理解能力，还考查了勾股定理在空间的应用，综合性较强．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
下列式子正确的是（ ）
| A、（-0.2）-2=25 | ||||
B、（-
| ||||
| C、（-2）-3=-8 | ||||
D、（-
|
下列各式计算结果正确的是（ ）
A、
| ||
B、
| ||
C、-
| ||
D、±
|
下列数据3，2，3，4，5，2，2的众数和中位数是（ ）
| A、2，4 | B、2，3 |
| C、3，4 | D、3，3 |
鞋柜中有3双鞋，任取一只恰为左脚的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在平面直角坐标系中，描出下列各点：A（1，1），B（5，1），C（3，3），D（-3，3），E（-2，2），F（-2，-4），G（5，0），H（3，-4），I（-1，-4），J（3，-2）．
在下列所给的三幅图案中再添画一个小正方形，使得每一个所构成的新图案都是轴对称图形．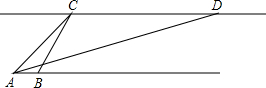
有全国最佳深水岸线资源的宁波拥有丰富的海洋资源，为了科学利用海洋资源，发展海洋经济．市政府对A，B两岛屿的海洋资源进行了可持续开发研究．用某勘测飞机测量两岛屿A，B之间的距离．飞机在高空点C处测得岛屿A的俯角∠ECA为45°，岛屿B的俯角∠ECB为60°，然后沿着平行于AB的方向水平飞行了1200海里到点D处，在点D处测得岛屿A的俯角∠EDA为30°，请你根据以上数据，解决下面两个问题：