题目内容
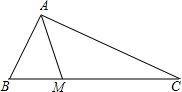 如图,在直角△ABC中,∠BAC=90°,AB=3,M是边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好在边AC的中点处,那么点M到AC的距离是
如图,在直角△ABC中,∠BAC=90°,AB=3,M是边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好在边AC的中点处,那么点M到AC的距离是
- A.1.5
- B.2
- C.2.5
- D.3
B
分析:作ME⊥AC,证明△CEM∽△CAB,然后利用折叠的性质和相似三角形的性质列出方程解答.
解答:如图,作ME⊥AC于E,则∠MEC=90°,
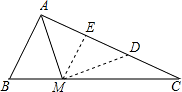 又∵在Rt△ABC中,∠BAC=90°,
又∵在Rt△ABC中,∠BAC=90°,
∴∠MEC=∠BAC,
∴ME∥AB,
∴∠BAM=∠EMA=45°(两直线平行,内错角相等),
∵∠BAM=∠MAC=45°,
∴∠MAE=∠AME=45°,
∴ME=AE,
∵ME∥AB,
∴△CEM∽△CAB,
∴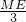 =
= ,
,
解得:ME=2,
所以点M到AC的距离是2.
故选B.
点评:本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、平行线和相似三角形判定和性质求解.
分析:作ME⊥AC,证明△CEM∽△CAB,然后利用折叠的性质和相似三角形的性质列出方程解答.
解答:如图,作ME⊥AC于E,则∠MEC=90°,
 又∵在Rt△ABC中,∠BAC=90°,
又∵在Rt△ABC中,∠BAC=90°,∴∠MEC=∠BAC,
∴ME∥AB,
∴∠BAM=∠EMA=45°(两直线平行,内错角相等),
∵∠BAM=∠MAC=45°,
∴∠MAE=∠AME=45°,
∴ME=AE,
∵ME∥AB,
∴△CEM∽△CAB,
∴
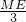 =
= ,
,解得:ME=2,
所以点M到AC的距离是2.
故选B.
点评:本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、平行线和相似三角形判定和性质求解.

练习册系列答案
相关题目
 如图,在直角△ABC中,∠C=90°、AB=6、AC=3,⊙O与边AB相切于点D、与边AC交于点E,连接DE,若DE∥BC,AE=2EC,则⊙O的半径是
如图,在直角△ABC中,∠C=90°、AB=6、AC=3,⊙O与边AB相切于点D、与边AC交于点E,连接DE,若DE∥BC,AE=2EC,则⊙O的半径是 如图,在直角△ABC中,∠C=90°,AB的垂直平分线交AB于D,交AC于F,且BE平分∠ABC,则∠A=( )
如图,在直角△ABC中,∠C=90°,AB的垂直平分线交AB于D,交AC于F,且BE平分∠ABC,则∠A=( ) 如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,DE垂直平分AB.
如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,DE垂直平分AB. 如图.在直角△ABC中,已知∠ACB=90°,CD⊥AB于点D,则下列关系不一定成立的是( )
如图.在直角△ABC中,已知∠ACB=90°,CD⊥AB于点D,则下列关系不一定成立的是( ) 如图,在直角△ABC中,∠A=90°,BC边上的垂直平分线交AC于点D;BD平分∠ABC,已知AC=m+2n,BC=2m+2n,则△BDE的周长为
如图,在直角△ABC中,∠A=90°,BC边上的垂直平分线交AC于点D;BD平分∠ABC,已知AC=m+2n,BC=2m+2n,则△BDE的周长为