题目内容
如图，P为⊙O外一点，则∠P=________度．
40
分析：根据圆周角定理求出∠ACB和∠BDA的度数，进而在四边形CEDP中求出∠P的度数．
解答：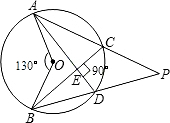
解：因为∠ADB=∠ACB=
∠AOB=×130°=65°，
所以∠BCP=∠EDP=180°-65°=115°，
又因为∠CED=90°，
所以∠P=360°-90°-115°-115°=40°．
点评：此题图形较复杂，综合考查了圆周角定理和四边形的内角和定理等内容，难度不大．
分析：根据圆周角定理求出∠ACB和∠BDA的度数，进而在四边形CEDP中求出∠P的度数．
解答：
解：因为∠ADB=∠ACB=∠AOB=×130°=65°，所以∠BCP=∠EDP=180°-65°=115°，
又因为∠CED=90°，
所以∠P=360°-90°-115°-115°=40°．
点评：此题图形较复杂，综合考查了圆周角定理和四边形的内角和定理等内容，难度不大．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
10、如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA=5，则△PCD的周长为（ ）
已知如图，P为⊙O外一点，过点P作⊙O的切线，切点为C，过P，O两点作⊙O的割线交⊙O于A、B两点，且PC=4cm，PA=3cm，则⊙O的半径R=
如图，P为圆外一点，PA切圆于A，PA=8，直线PCB交圆于C、B，且PC=4，连接AB、AC，∠ABC=α，∠ACB=β，则
如图，P为⊙O外一点，PA切⊙O于点A，且OP=5，PA=4，则sin∠APO=
如图，P为⊙O外一点，过点P作⊙O的两条割线，分别交⊙O于A、B和C、D，且AB为⊙O的直径，已知PA=AO=2cm，弧AC=弧CD，则PC的长为（ ）