Question

   如图，二次函数y=ax²+bx+c的图像与x轴的交点为A、D(A在D的右侧），与y轴的交点为C，且A(4，0)．C(0，-3)，对称轴是直线x=l． 

    (1)求二次函数的解析式； 

    (2)若M是第四象限抛物线上一动点，且横坐标为m，设四边形OCMA的面积为s．请写出s与m之间的函数关系式，并求出当m为何值时，四边形OCMA的面积最大；

    (3)设点B是x轴上的点，P是抛物线上的点，是否存在点P，使得以A，B、C，P四点为顶点的四边形为平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由.

Answer 1

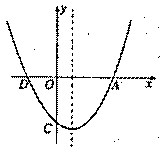
解；(1)∵A(4，0)，对称轴是直线x=l．∴D（-2，0），

  ∵C(0,-3)∴c=-3,16a+4b-3=0,4a-2b-3=0.

  解得．A=，b=-，∴二次函数解析式为：y=x² -x-3……（4分）

  (2)连接AC，直线AC的解析式y=x-3，过M作MF⊥x轴于F，交CA于E，设

  M(m，m² -m-3)，E(m,m-3),则ME=m²+m，s=S_△AOC+S_△ACM=

  6+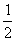×4× EM= 6+2（m²+m）=-m²+3m+6,m=2时，s最大。……（8分）

  (3)存在，P(2，-3)或P(1+，3)或P(1-，3)……（11分）