题目内容
1．一个多边形的外角和是它的内角和的$\frac{1}{4}$，求这个多边形的边数．分析 首先设这个多边形的边数为n，由题意得等量关系：此多边形的内角和×$\frac{1}{4}$=外角和，根据等量关系，列出方程，再解即可．
解答 解：设这个多边形的边数为n，由题意得：
180（n-2）×$\frac{1}{4}$=360，
解得：n=10，
答：这个多边形的边数为10．
点评 此题主要考查了多边形的内角与外角，关键是掌握多边形内角和定理：（n-2）•180°（n≥3）且n为整数），外角和是360°．
练习册系列答案
相关题目
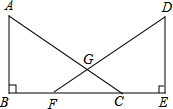已知，如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AC=DF，BF=CE．求证：AB=DE．
如图所示，在直角坐标系中，四边形OABC各顶点的坐标分别是O（0，0），A（2，3），B（5，4），C（8，2），试确定这个四边形的面积．