题目内容

6．抛物线y=-（x-1）（x-2）的顶点坐标是（$\frac{3}{2}$，$\frac{1}{4}$）．

分析 把二次函数化为顶点式得出顶点坐标可．

解答 解：∵y=-（x-1）（x-2）=-（x-$\frac{3}{2}$）2+$\frac{1}{4}$，
∴顶点坐标是（$\frac{3}{2}$，$\frac{1}{4}$）．
故答案为：（$\frac{3}{2}$，$\frac{1}{4}$）．

点评 本题考查了二次函数的性质，熟悉顶点式y=a（x-h）2+k（a≠0）是解题的关键．

练习册系列答案
相关题目
16．计算并观察下列式子，探索它们的规律，并解决问题．
$（\sqrt{3}+\sqrt{1}）（\sqrt{3}-\sqrt{1}）$=2．
$（\sqrt{5}+\sqrt{3}）（\sqrt{5}-\sqrt{3}）$=2．
$（\sqrt{7}+\sqrt{5}）（\sqrt{7}-\sqrt{5}）$=2．
…
（1）试用正整数n表示这个规律，并加以证明；
（2）求$\frac{1}{{\sqrt{3}+1}}+\frac{1}{{\sqrt{5}+\sqrt{3}}}+\frac{1}{{\sqrt{7}+\sqrt{5}}}+…+\frac{1}{{\sqrt{121}+\sqrt{119}}}$的值．
17．一个多边形，每个外角相等．它的内角和与外角和的和等于720°，则这个多边形的每一个外角等于多少度？
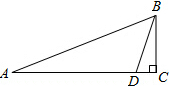14．一艘军舰从点A向位于正东方向的C岛航行，在点A处测得B岛在其北偏东70°方向，航行75千米到达点D处，测得B岛在其北偏东20°，继续航行5千米到达C岛，此时接到通知，要求这艘军舰在半小时内赶到正北方向的B岛执行任务，则这艘军舰的航行速度至少为多少才能按时赶到B岛？
1．已知m+n=2，求m2+mn+2n的值．
11．已知一元二次方程ax2+bx+c=0的两个根是x1=-1，x2=4．则一元二次方程a（x-2）2+b（x-2）+c=0的两个根是（　　）
A．x1=x2=2B．x1=1，x2=6C．x1=-3，x2=2D．无法确定
18．若关于x，y（x≠0，x≠1，y≠0，y≠1）的单项式x4ya与（-xby）2的乘积为x16y4，求ab的值．
15．将下列算式补充完整，并在下面的算式后填上所使用的法则或运算律．
（-7）-（+10）+（-4）-（-5）+6=（-7）+（-10）+（-4）+5+6（统一成加法）
=-7-10一4+5+6（化为代数和）
=-（-7-10-4）+（5+6）（加法结合律和结合律）
=-21+11（加法的计算法则）
=-10（加法的计算法则）．
16．把下列算式写成省略括号的形式：（+5）-（+8）+（-2）-（-3）+（+7）=5-8-2+3+7．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网