题目内容
若方程x2-kx+4=0有两个相等的实数根，求出k的值并求出此时方程的根．
考点：根的判别式
专题：
分析：根据方程有两个相等的实数根得出△=（-k）2-4×1×4=0，求出k的值，再代入方程，求出方程的解即可．
解答：解：∵方程x2-kx+4=0有两个相等的实数根，
∴△=（-k）2-4×1×4=0，
解得：k=±4，
①当k=4时，方程为：x2-4x+4=0，
解得：x1=x2=2；
②当k=-4时，方程为：x2+4x+4=0，
解得：x1=x2=-2．
∴△=（-k）2-4×1×4=0，
解得：k=±4，
①当k=4时，方程为：x2-4x+4=0，
解得：x1=x2=2；
②当k=-4时，方程为：x2+4x+4=0，
解得：x1=x2=-2．
点评：本题考查了根的判别式和解一元二次方程的应用，解此题的关键是求出k的值，题目比较好，难度适中．
练习册系列答案
名校课堂系列答案
相关题目
如图，△ABC≌△BAD，AC与BD是对应边，AC=8cm，AD=10cm，DE=CE=2cm，那么AE的长是运算结果为1-2x2+x4的是（ ）
| A、（-1+x2）2 |
| B、（1+x2）2 |
| C、（-1-x2）2 |
| D、（1-x）2 |
下列说法中，正确的是（ ）
| A、有最小的有理数 |
| B、有最小的负数 |
| C、有绝对值最小的数 |
| D、有最小的正数 |
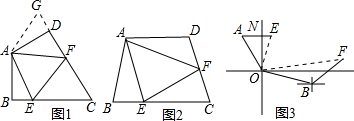
（1）有理数a，b，c在数轴上的位置如图所示：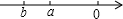
已知a，b两数在数轴上对应的点如图所示，在下列结论：①a＞b；②a+b＞0；③a-b＞0；④ab＜0；⑤