题目内容
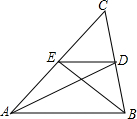 如图,△ABC中,E、D分别是AC、BC的中点,则S△CDE:SABDE=( )
如图,△ABC中,E、D分别是AC、BC的中点,则S△CDE:SABDE=( )| A、1:4 | B、2:3 |
| C、1:3 | D、1:2 |
考点:三角形中位线定理,相似三角形的判定与性质
专题:
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥AB,DE=
AB,然后求出△ABC和△EDC相似,根据相似三角形面积的比等于相似比的平方求出两三角形的面积的比,然后求解即可.
| 1 |
| 2 |
解答:解:∵E、D分别是AC、BC的中点,
∴DE是△ABC的中位线,
∴DE∥AB,DE=
AB,
∴△ABC∽△EDC,
∴S△EDC=4S△ABC,
∴S△CDE:SABDE=1:(4-1)=1:3.
故选C.
∴DE是△ABC的中位线,
∴DE∥AB,DE=
| 1 |
| 2 |
∴△ABC∽△EDC,
∴S△EDC=4S△ABC,
∴S△CDE:SABDE=1:(4-1)=1:3.
故选C.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,相似三角形的判定与性质,熟记定理并求出三角形相似是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列图案中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列各数中,与(-2-3)5相等的是( )
| A、(-2)5+(-3)5 |
| B、(-2)5-35 |
| C、-55 |
| D、55 |
新定义运算a*b=a(a-b),则3*4的结果是( )
| A、12 | B、4 | C、3 | D、-3 |
 在平行四边形ABCD中,点E为AD的中点,连接CE,点M、N为CE上两点,且BM∥DN.连接DM并延长交AB于F,若BF=2AF,求
在平行四边形ABCD中,点E为AD的中点,连接CE,点M、N为CE上两点,且BM∥DN.连接DM并延长交AB于F,若BF=2AF,求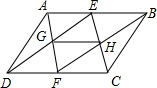 如图所示,在?ABCD中,点E、F分别是AB、CD的中点,连接AF、DE、BF、CE,AF与DE交于点G,BF与CE交于点H,连接GH,求证:GH∥DC且GH=
如图所示,在?ABCD中,点E、F分别是AB、CD的中点,连接AF、DE、BF、CE,AF与DE交于点G,BF与CE交于点H,连接GH,求证:GH∥DC且GH=