题目内容
(1)如图1,正方形的面积为S,两对边与两条对角线围成的两个三角形的面积分别为S1和S2,则 、
、 、
、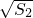 三者之间的数量关系为______;
三者之间的数量关系为______;
(2)如图2,若将正方形改为矩形,其它不变,上述 、
、 、
、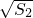 三者之间的数量关系还成立吗?
三者之间的数量关系还成立吗?
回答:______;
(3)如图3,若将矩形改为平行四边形,其它不变,上述 、
、 、
、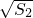 三者之间的数量关系还成立吗?回答:______;
三者之间的数量关系还成立吗?回答:______;
(4)如图4,梯形的面积为S,两底边与两条对角线围成的两个三角形的面积分别为S1和S2,则 、
、 、
、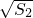 三者是否还存在上述的数量关系?若存在,请你给出证明;若不成立,请说明理由.
三者是否还存在上述的数量关系?若存在,请你给出证明;若不成立,请说明理由.

解:(1)正方形的对角线把正方形分成全等的四个等腰直角三角形,所以设正方形的面积为1,那么S1,S2的面积均为 ,∴
,∴ =
= +
+ ;
;
(2)矩形的对角线互相平分且相等,可得矩形的对角线把矩形分成面积相等的4部分,所以设矩形的面积为1,那么S1,S2的面积均为 ,∴
,∴ =
= +
+ ;
;
(3)由平行四边形的对角线互相平分可得平行四边形的对角线把平行四边形分成面积相等的4部分,所以设平行四边形的面积为1,那么S1,S2的面积均为 ,∴
,∴ =
= +
+ ;
;
(4)设梯形的面积为1,上底为a,下底为b,高为h,易得S1,S2所在的两三角形相似,那么S1所在的三角形的高为 ,S2所在的三角形的高为
,S2所在的三角形的高为 ,利用面积公式,整理后可得
,利用面积公式,整理后可得 =
= +
+ .
.
分析:(1)设正方形的面积为1,那么可得S1,S2的面积均为 ,可得
,可得 、
、 、
、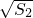 三者之间的数量关系;
三者之间的数量关系;
(2)同法可得矩形中 、
、 、
、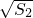 三者之间的数量关系;
三者之间的数量关系;
(3)同理可得平行四边形中 、
、 、
、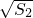 三者之间的数量关系;
三者之间的数量关系;
(4)可设梯形的面积为1,易得S1与S2相似,高的比为上下底的比,那么可得 、
、 、
、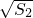 三者之间的数量关系.
三者之间的数量关系.
点评:本题综合考查了各种四边形的面积问题,解决本题的关键是利用所给特殊图形的性质得到各面积的算术平方根的关系;难点是利用类比的性质得到相应规律求解.
 ,∴
,∴ =
= +
+ ;
;(2)矩形的对角线互相平分且相等,可得矩形的对角线把矩形分成面积相等的4部分,所以设矩形的面积为1,那么S1,S2的面积均为
 ,∴
,∴ =
= +
+ ;
;(3)由平行四边形的对角线互相平分可得平行四边形的对角线把平行四边形分成面积相等的4部分,所以设平行四边形的面积为1,那么S1,S2的面积均为
 ,∴
,∴ =
= +
+ ;
;(4)设梯形的面积为1,上底为a,下底为b,高为h,易得S1,S2所在的两三角形相似,那么S1所在的三角形的高为
 ,S2所在的三角形的高为
,S2所在的三角形的高为 ,利用面积公式,整理后可得
,利用面积公式,整理后可得 =
= +
+ .
.分析:(1)设正方形的面积为1,那么可得S1,S2的面积均为
 ,可得
,可得 、
、 、
、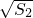 三者之间的数量关系;
三者之间的数量关系;(2)同法可得矩形中
 、
、 、
、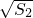 三者之间的数量关系;
三者之间的数量关系;(3)同理可得平行四边形中
 、
、 、
、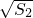 三者之间的数量关系;
三者之间的数量关系;(4)可设梯形的面积为1,易得S1与S2相似,高的比为上下底的比,那么可得
 、
、 、
、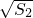 三者之间的数量关系.
三者之间的数量关系.点评:本题综合考查了各种四边形的面积问题,解决本题的关键是利用所给特殊图形的性质得到各面积的算术平方根的关系;难点是利用类比的性质得到相应规律求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
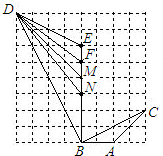 如图,在正方形网格上,与△ABC相似的三角形是( )
如图,在正方形网格上,与△ABC相似的三角形是( )| A、△NBD | B、△MBD | C、△EBD | D、△FBD |
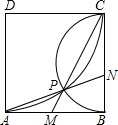 如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于( )
如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
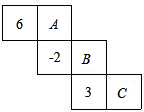 如图,是正方形的表面展形图,如果相对两个面数字之和相等,且A+B+C=14,则6A-2B+3C=
如图,是正方形的表面展形图,如果相对两个面数字之和相等,且A+B+C=14,则6A-2B+3C=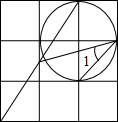 如图,在正方形网格图中,每个小正方形的边长均为 1,则∠1的正弦值是
如图,在正方形网格图中,每个小正方形的边长均为 1,则∠1的正弦值是 如图,在正方形ABCD中,E是BC上一点,且BC:EC=4:1,F是DC的中点.
如图,在正方形ABCD中,E是BC上一点,且BC:EC=4:1,F是DC的中点.