题目内容
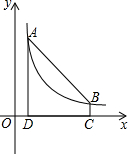 如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
考点:待定系数法求反比例函数解析式,反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
专题:代数几何综合题,待定系数法
分析:(1)根据题意列出关于m与n的方程组,求出方程组的解得到m与n的值,确定出A与B坐标,设出反比例函数解析式,将A坐标代入即可确定出解析式;
(2)存在,设E(x,0),表示出DE与CE,连接AE,BE,三角形ABE面积=四边形ABCD面积-三角形ADE面积-三角形BCE面积,求出即可.
(2)存在,设E(x,0),表示出DE与CE,连接AE,BE,三角形ABE面积=四边形ABCD面积-三角形ADE面积-三角形BCE面积,求出即可.
解答: 解:(1)由题意得:
解:(1)由题意得:
,
解得:
,
∴A(1,6),B(6,1),
设反比例函数解析式为y=
,
将A(1,6)代入得:k=6,
则反比例解析式为y=
;
(2)存在,
设E(x,0),则DE=x-1,CE=6-x,
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
连接AE,BE,
则S△ABE=S四边形ABCD-S△ADE-S△BCE
=
(BC+AD)•DC-
DE•AD-
CE•BC
=
×(1+6)×5-
(x-1)×6-
(6-x)×1
=
-
x=5,
解得:x=5,
则E(5,0).
 解:(1)由题意得:
解:(1)由题意得:
|
解得:
|
∴A(1,6),B(6,1),
设反比例函数解析式为y=
| k |
| x |
将A(1,6)代入得:k=6,
则反比例解析式为y=
| 6 |
| x |
(2)存在,
设E(x,0),则DE=x-1,CE=6-x,
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
连接AE,BE,
则S△ABE=S四边形ABCD-S△ADE-S△BCE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 35 |
| 2 |
| 5 |
| 2 |
解得:x=5,
则E(5,0).
点评:此题考查了待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )
| A、1:2 | B、2:1 |
| C、1:4 | D、4:1 |
 巴中市对初三年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A,B,C,D四个等级.现抽取这三种成绩共1000份进行统计分析,其中A,B,C,D分别表示优秀,良好,合格,不合格四个等级.相关数据统计如下表及图所示.
巴中市对初三年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A,B,C,D四个等级.现抽取这三种成绩共1000份进行统计分析,其中A,B,C,D分别表示优秀,良好,合格,不合格四个等级.相关数据统计如下表及图所示.
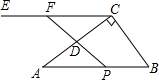 如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,D是AC中点,CD∥BA,动点P以每秒1个单位长的速度从点B出发向点A移动,连接PD并延长交CE于点F,设点P移动时间为t秒.
如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,D是AC中点,CD∥BA,动点P以每秒1个单位长的速度从点B出发向点A移动,连接PD并延长交CE于点F,设点P移动时间为t秒.
 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD.若∠A=25°,则∠C=
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD.若∠A=25°,则∠C=