题目内容
某商场以每台360元的价格购进一批计算器,原售价每台600元,现为了促销,商场采取如下方式:买一台单价为590元,买两台每台都为580元,依此类推,即每多买一台则所买各台单价均再减10元,但最低不能低于每台400元.某单位一次性购买该计算器x台,实际购买单价为y元.(x为正整数)
(1)求y与x的函数关系式;
(2)若该单位一次性购买该计算器不超过20台,购买多少台时,商场获利最大?最大利润是多少?
(1)求y与x的函数关系式;
(2)若该单位一次性购买该计算器不超过20台,购买多少台时,商场获利最大?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)根据题意可得出实际购买单价=原价-10x,进而得出答案;
(2)根据销量乘以每台利润进而得出总利润,即可求出即可.
(2)根据销量乘以每台利润进而得出总利润,即可求出即可.
解答:解:(1)∵原售价每台600元,现为了促销,商场采取如下方式:买一台单价为590元,买两台每台都为580元,
依此类推,即每多买一台则所买各台单价均再减10元,
∴y与x的函数关系式为:y=-10x+600(0≤x≤20);
(2)设商场获利为W元,购买x台时,商场获利最大,
则W=x(-10x+600-360)
=-10x2+240x
=-10(x-12)2+1440,
∴当x=12时,W最大值=1440.
依此类推,即每多买一台则所买各台单价均再减10元,
∴y与x的函数关系式为:y=-10x+600(0≤x≤20);
(2)设商场获利为W元,购买x台时,商场获利最大,
则W=x(-10x+600-360)
=-10x2+240x
=-10(x-12)2+1440,
∴当x=12时,W最大值=1440.
点评:此题主要考查了二次函数的应用,根据题意得出W与x的函数关系是解题关键.

练习册系列答案
相关题目
下列函数
(1)y=πx;(2)y=2x-1;(3)y=
;(4)y=2-1-3x.
是一次函数的有( )
(1)y=πx;(2)y=2x-1;(3)y=
| 1 |
| x |
是一次函数的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
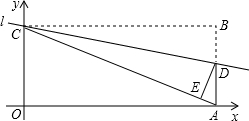 在直角坐标系中,四边形OABC为矩形,直线l:y=-
在直角坐标系中,四边形OABC为矩形,直线l:y=- 如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.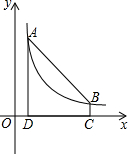 如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.