题目内容
4.学校国旗护卫队成员的身高分布如下表:| 身高/cm | 159 | 160 | 161 | 162 |
| 人数 | 7 | 10 | 9 | 9 |
| A. | 160和160 | B. | 160和160.5 | C. | 160和161 | D. | 161和161 |
分析 众数是一组数据中出现次数最多的数据;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.
解答 解:数据160出现了10次,次数最多,众数是:160cm;
排序后位于中间位置的是161cm,中位数是:161cm.
故选C.
点评 本题为统计题,考查众数与中位数的意义.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
14.已知直线y=$\frac{1}{2}$x+k-4与抛物线y=x2-4kx-3k+4k2的对称轴的交点在第四象限,则k的取值范围是( )
| A. | k>0 | B. | k<2 | C. | 0<k<2 | D. | -2<k<0 |
15.某校举办诗词大会有4名女生和6名男生获奖,现从中任选1人去参加区诗词大会,则选中女生的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
12.某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
| 时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
| 售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
| 销量(斤) | 80-3x | 120-x | |
| 储存和损耗费用(元) | 40+3x | 3x2-64x+400 | |
16.某商店分两次购进 A、B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
(1)求A、B两种商品每件的进价分别是多少元?
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
| 购进数量(件) | 购进所需费用(元) | ||
| A | B | ||
| 第一次 | 30 | 40 | 3800 |
| 第二次 | 40 | 30 | 3200 |
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)
如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)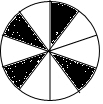 如图所示的圆形纸板被等分成10个扇形挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{2}{5}$.
如图所示的圆形纸板被等分成10个扇形挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{2}{5}$.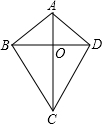 如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中: