题目内容
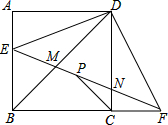 如图所示正方形ABCD,点E为AB上一点,在BC的延长线上截取CF=AE,EF与BD、CD分别交于点M、N,P为EF的中点,下列结论正确的个数为
如图所示正方形ABCD,点E为AB上一点,在BC的延长线上截取CF=AE,EF与BD、CD分别交于点M、N,P为EF的中点,下列结论正确的个数为①∠EDB=∠EFB;②DM=DN;③∠DNE=∠BDF;④CP⊥BD.
考点:全等三角形的判定与性质,正方形的性质
专题:
分析:根据正方形的性质得出DC=AD,∠ADC=∠ABC=90°,∠A=∠DCF=90°,根据SAS推出△EAD≌△FCD,根据全等三角形的性质得出DE=DF,∠ADE=∠FDC,求出△EDF是等腰直角三角形,推出E、B、F、D四点共圆,即可判断①;由三角形外角性质得出∠DMN=∠BDE+45°,∠DNM=45°+∠CDF=45°+∠ADE,即可判断②;根据∠DNE=45°+∠CDF=∠BDF即可判断③;连接DP、BP,求出DP=BP=
EF,推出△BCP≌△DCP,根据全等得出∠DCP=∠BCP,根据等腰三角形的性质推出CP⊥BD,即可判断④正确.
| 1 |
| 2 |
解答:解:∵四边形ABCD是正方形,
∴DC=AD,∠ADC=∠ABC=90°,∠A=∠DCF=90°,
在△EAD和△FCD中,
,
∴△EAD≌△FCD(SAS),
∴DE=DF,∠ADE=∠FDC,
∵∠ADC=90°,
∴∠EDF=∠EDC+∠CDF=∠EDC+∠ADE=∠DC=90°,
即△EDF是等腰直角三角形,
∵∠ABC=90°,
∴∠EDF+∠ABC=180°,
∴E、B、F、D四点共圆,
∴∠EDB=∠EFB,∴①正确;
∵△EDF是等腰直角三角形,
∴∠DEF=∠DFE=45°,
由三角形外角性质得:∠DMN=∠BDE+45°,∠DNM=45°+∠CDF=45°+∠ADE,
根据已知不知道∠BDE和∠ADE是否相等,
∴∠DMN和∠DNM不能推出相等,即DM=DN不一定正确,∴②错误;
∠DNE=45°+∠CDF=∠BDF,∴③正确;
连接DP、BP,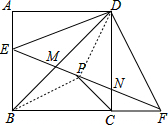
则∵∠EDF=∠EBC=90°,P位EF的中点,
∴DP=BP=
EF,
在△BCP和△DCP中,
,
∴△BCP≌△DCP(SSS),
∴∠DCP=∠BCP,
∵DC=BC,
∴CP⊥BD(三线合一),∴④正确;
故答案为:①③④.
∴DC=AD,∠ADC=∠ABC=90°,∠A=∠DCF=90°,
在△EAD和△FCD中,
|
∴△EAD≌△FCD(SAS),
∴DE=DF,∠ADE=∠FDC,
∵∠ADC=90°,
∴∠EDF=∠EDC+∠CDF=∠EDC+∠ADE=∠DC=90°,
即△EDF是等腰直角三角形,
∵∠ABC=90°,
∴∠EDF+∠ABC=180°,
∴E、B、F、D四点共圆,
∴∠EDB=∠EFB,∴①正确;
∵△EDF是等腰直角三角形,
∴∠DEF=∠DFE=45°,
由三角形外角性质得:∠DMN=∠BDE+45°,∠DNM=45°+∠CDF=45°+∠ADE,
根据已知不知道∠BDE和∠ADE是否相等,
∴∠DMN和∠DNM不能推出相等,即DM=DN不一定正确,∴②错误;
∠DNE=45°+∠CDF=∠BDF,∴③正确;
连接DP、BP,

则∵∠EDF=∠EBC=90°,P位EF的中点,
∴DP=BP=
| 1 |
| 2 |
在△BCP和△DCP中,
|
∴△BCP≌△DCP(SSS),
∴∠DCP=∠BCP,
∵DC=BC,
∴CP⊥BD(三线合一),∴④正确;
故答案为:①③④.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质,正方形的性质和判定的应用,能综合运用性质进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等,难度偏大.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
若一辆汽车在a秒内行驶了
米,则它在2分钟内行驶了( )
| m |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
2013年11月11日某淘宝卖家卖出两件商品,它们的售价均为120元,其中一件盈利20%,一件亏损20%,在这次买卖中这位卖家( )
| A、不赔不赚 | B、赔了10元 |
| C、赚了10元 | D、赔了50元 |
三角形内切圆的圆心是三角形的( )
| A、外心 | B、重心 | C、内心 | D、垂心 |
 将△ABC向下平移5个单位长度.
将△ABC向下平移5个单位长度.