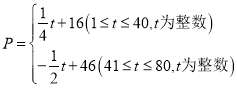题目内容
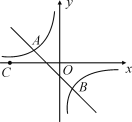
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,
,![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
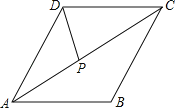
,点![]() 在抛物线上,
在抛物线上,![]() 轴,且
轴,且![]() .
.
(1)求点![]() ,
,![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)点![]() 为
为![]() 轴右侧抛物线上一点.
轴右侧抛物线上一点.
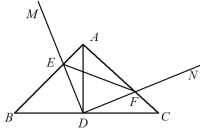
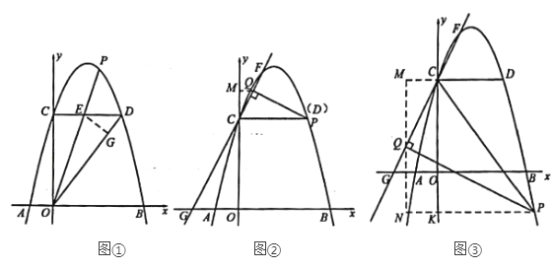
①如图①,若![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,求点
,求点![]() 的坐标;
的坐标;
②如图②,抛物线上一点![]() 的横坐标为2,直线
的横坐标为2,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)令y=0,解方程即可求出点A、B的坐标,由此可求得AB的长及对称轴,再根据![]() 即可求得OD长,根据对称轴即可求得CD=6,再根据勾股定理即可求得点C坐标,将点C坐标代入函数关系式从而可求得a的值;
即可求得OD长,根据对称轴即可求得CD=6,再根据勾股定理即可求得点C坐标,将点C坐标代入函数关系式从而可求得a的值;
(2)①作![]() 于
于![]() ,根据
,根据![]() 平分
平分![]() 可得
可得![]() ,进而设
,进而设![]() ,根据
,根据![]() 可得方程
可得方程![]() 求解即可求得点E坐标为
求解即可求得点E坐标为![]() ,再用待定系数法求得直线OP的函数关系式,与二次函数关系式联立方程组即可求得点P坐标;
,再用待定系数法求得直线OP的函数关系式,与二次函数关系式联立方程组即可求得点P坐标;
②分两种情形(Ⅰ)若点![]() 在
在![]() 点上方,如图②,(Ⅱ)若点
点上方,如图②,(Ⅱ)若点![]() 在点
在点![]() 下方,如图③,分别列出方程即可解决.
下方,如图③,分别列出方程即可解决.
解:(1)令![]() ,则
,则![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∵![]()
∴![]() ,
,
∵点C在y轴上且![]() 轴,
轴,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴点![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①作![]() 于
于![]() ,
,
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
设![]() 对应函数表达式为
对应函数表达式为![]() ,
,
把![]() 代入,得
代入,得![]() ,
,
∴![]() 对应函数表达式为
对应函数表达式为![]() .
.
∵![]() ,
,
∴二次函数表达式为![]() ,
,
∴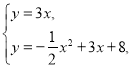 ,
,
解得![]() 或
或![]() (舍去)
(舍去)
∴点![]() .
.
②∵当![]() 时,
时,![]() ,∴点
,∴点![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]()
把点![]() 、点
、点![]() 代入,
代入,
得![]()
解得![]()
∴直线![]() 的函数表达式为
的函数表达式为![]() ,
,
∴点![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅰ)若点![]() 在
在![]() 点上方,如图②.
点上方,如图②.
过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() .
.
∵![]() ,
,
∴![]() 轴,
轴,
∵![]() 轴,
轴,
∴点![]() 与点
与点![]() 重合,
重合,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴设![]() ,
,![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
∴![]() .
.
把![]() 代入
代入![]()
得,![]() .
.
∴![]() .
.
(Ⅱ)若点![]() 在点
在点![]() 下方,如图③.
下方,如图③.
过点![]() 作
作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 轴于点
轴于点![]() .
.
∴![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]()
∵![]() 轴,
轴,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴设![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() ,得
,得
![]() ,
,
∴![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,
代入![]() 得
得
![]() ,
,
∴![]() .
.
综上所述,![]() 或
或![]() .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案