Question

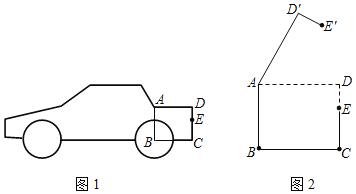
【题目】图1是某小型汽车的侧面示意图，其中矩形ABCD表示该车的后备箱，在打开后备箱的过程中，箱盖ADE可以绕点A逆时针方向旋转，当旋转角为60°时，箱盖ADE落在AD′E′的位置（如图2所示）．已知AD＝96厘米，DE＝28厘米，EC＝42厘米．

（1）求点D′到BC的距离；

（2）求E、E′两点的距离．

Answer 1

【答案】（1）（48+70）厘米．（2）100厘米

【解析】

（1）过点作，垂足为点，交于点，利用旋转的性质可得出厘米，，利用矩形的性质可得出，在△中，通过解直角三角形可求出的长，结合及可求出点到的距离；

（2）连接，，，利用旋转的性质可得出，，进而可得出是等边三角形，利用等边三角形的性质可得出，在中，利用勾股定理可求出的长度，结合可得出、两点的距离．

解：（1）过点D′作D′H⊥BC，垂足为点H，交AD于点F，如图3所示．

由题意，得：AD′＝AD＝96厘米，∠DAD′＝60°．

∵四边形ABCD是矩形，

∴AD∥BC，

∴∠AFD′＝∠BHD′＝90°．

在△中，（厘米）．

又∵CE＝42厘米，DE＝28厘米，

∴FH＝DC＝DE+CE＝70厘米，

厘米．

答：点到的距离为厘米．

（2）连接AE，AE′，EE′，如图4所示．

由题意，得：AE′＝AE，∠EAE′＝60°，

∴△AEE′是等边三角形，

∴EE′＝AE．

∵四边形ABCD是矩形，

∴∠ADE＝90°．

在Rt△ADE中，AD＝96厘米，DE＝28厘米，

（厘米），

∴EE′＝100厘米．

答：E、E′两点的距离是100厘米．