题目内容
如图，矩形ABCD中，AB=6，BC=8，对角线AC、BD相交于O，以O为圆心，5为半径画圆，则A、B、C、D中共有（ ）个点在⊙O上．| A、1 | B、2 | C、3 | D、4 |
考点：点与圆的位置关系
专题：
分析：首先根据矩形的性质以及勾股定理得出AO=CO=BO=DO=5，即可得出A、B、C、D都在⊙O上．
解答：解：∵矩形ABCD中，AB=6，BC=8，
∴AC=BD=
=10，
∴AO=CO=BO=DO=5，
∵以O为圆心，5为半径画圆，
则A、B、C、D中共有4个点都在⊙O上．
故选：D．
∴AC=BD=
| 82+62 |
∴AO=CO=BO=DO=5，
∵以O为圆心，5为半径画圆，
则A、B、C、D中共有4个点都在⊙O上．
故选：D．
点评：此题主要考查了矩形的性质以及点与圆的位置关系，根据已知得出AO=CO=BO=DO=5是解题关键．
练习册系列答案
相关题目
下列叙述错误的是（ ）
| A、所有的命题都有条件和结论 |
| B、所有的命题都是定理 |
| C、所有的定理都是命题 |
| D、所有的公理都是真命题 |
下列运算正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、4
|
如图： |
| AB |
|
| CD |
| A、AB=2CD |
| B、AB＞2CD |
| C、AB＜2CD |
| D、无法确定 |
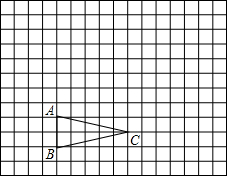如图，△ABC在方格纸中．
如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2013次碰到矩形的边时，点P的坐标为