题目内容
如图，PA、PB与⊙O切于A、B两点，PC是任意一条割线，且交⊙O于点E、C，交AB于点D．求证：
| AC2 |
| BC2 |
| AD |
| BD |
分析：由△PAC∽△PEA，得
=
，同理，
=
，再由△ACD∽△EBD，△AED∽△CBD，可得
=
，
=
，两式相乘即可得出结论．
| AC |
| AE |
| PC |
| PA |
| BC |
| BE |
| PC |
| PB |
| AC |
| BE |
| AD |
| ED |
| AE |
| BC |
| ED |
| BD |
解答：
解：如图，连接AE、BE，
由弦切角定理可知，∠PCA=∠PAE，
则△PAC∽△PEA，得
=
，
同理，
=
．
∵PA=PB，
∴
=
，
即
=
，
在⊙O中，由△ACD∽△EBD，△AED∽△CBD，
可得
=
，
=
，
从而
•
=
，
即
=
．
解：如图，连接AE、BE，由弦切角定理可知，∠PCA=∠PAE，
则△PAC∽△PEA，得
| AC |
| AE |
| PC |
| PA |
同理，
| BC |
| BE |
| PC |
| PB |
∵PA=PB，
∴
| AC |
| AE |
| BC |
| BE |
即
| AC |
| BC |
| AE |
| BE |
在⊙O中，由△ACD∽△EBD，△AED∽△CBD，
可得
| AC |
| BE |
| AD |
| ED |
| AE |
| BC |
| ED |
| BD |
从而
| AC |
| BC |
| AE |
| BE |
| AD |
| BD |
即
| AC2 |
| BC2 |
| AD |
| BD |
点评：本题考查了切线的性质、三角形的判定和性质，此题是一个综合题，难度较大．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
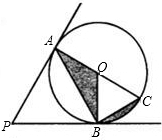如图，PA、PB与⊙O相切，切点分别为A、B，PA=3，∠P=60°，若AC为⊙O的直径，则图中阴影部分的面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、π |
如图，PA、PB与⊙O分别相切于点A、点B，AC是⊙O的直径，PC交⊙O于点D，已知∠APB=60°，AC=2，那么CD的长为
如图，PA、PB与⊙O相切，切点分别为A、B．PA=3，∠P=60°，若AC为⊙O的直径，则圆中阴影部分的面积为
B．
D．