题目内容
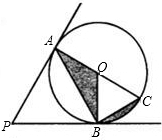如图，PA、PB与⊙O相切，切点分别为A、B，PA=3，∠P=60°，若AC为⊙O的直径，则图中阴影部分的面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、π |
分析：阴影部分的面积=扇形OBC的面积．
解答：解：∵PA、PB与⊙O相切，
∴PA=PB，∠PAO=∠PBO=90°
∵∠P=60°，
∴△PAB为等边三角形，∠AOB=120°
∴AB=PA=3，∠OBC=60°
∵OB=OC
∴△OBC为等边三角形
∴∠OCB=60°
∵AC为⊙O的直径，
∴∠ABC=90°．
∴OB=
．
∵OA=OC，
∴S△AOB=S△OBC
∴S阴影=S扇形OBC=
=
，
故选A．
∴PA=PB，∠PAO=∠PBO=90°
∵∠P=60°，
∴△PAB为等边三角形，∠AOB=120°
∴AB=PA=3，∠OBC=60°
∵OB=OC
∴△OBC为等边三角形
∴∠OCB=60°
∵AC为⊙O的直径，
∴∠ABC=90°．
∴OB=
| 3 |
∵OA=OC，
∴S△AOB=S△OBC
∴S阴影=S扇形OBC=
60π
| ||
| 360 |
| π |
| 2 |
故选A．
点评：阴影部分的面积往往能整理为一个规则图形的面积．
练习册系列答案
阅读快车系列答案
相关题目
如图，PA、PB与⊙O分别相切于点A、点B，AC是⊙O的直径，PC交⊙O于点D，已知∠APB=60°，AC=2，那么CD的长为
如图，PA、PB与⊙O切于A、B两点，PC是任意一条割线，且交⊙O于点E、C，交AB于点D．
如图，PA、PB与⊙O相切，切点分别为A、B．PA=3，∠P=60°，若AC为⊙O的直径，则圆中阴影部分的面积为
B．
D．