题目内容
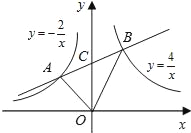
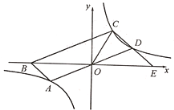
【题目】如图，在平面直角坐标系中，平行四边形ABCD的边AD经过O点，A、C、D三点都在反比例函数
的图像上，B点在
轴的负半轴上，延长CD交轴于点E，连接CO.
若C（1,2）,D(2,1)，则
为_______.
【答案】6
【解析】
根据C,D的坐标可求出S△CDO的值，再根据平行四边形的性质得出△AOB≌△DOE，故OD为△CEO的中线，则可求出△COE的面积，再利用平行四边形ABCD的面积等于△BEC的面积即可求解.
延长CD交x轴与点E，
∵C（1,2）,D(2,1)，
∴S△CDO=
=
∵四边形ABCD为平行四边形，A,D关于原点对称，∴△AOB≌△DOE，
故D点为CE中点，则S△COE=2S△CDO=3，
又O点为BE中点，
故
=S△BEC=2S△COE=6
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
