题目内容
 如图,在△OAB中,OA=OB=2,∠AOB=45°,C是AB中点,则点O关于点C的对称点的坐标是
如图,在△OAB中,OA=OB=2,∠AOB=45°,C是AB中点,则点O关于点C的对称点的坐标是分析:过点A作AD⊥OB于D,然后求出AD、OD的长,从而得到点A的坐标,再根据中点公式求出点C的坐标,然后利用中点公式求出点O关于点C的对称点即可.
解答: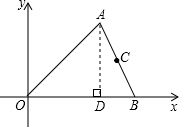 解:如图,过点A作AD⊥OB于D,
解:如图,过点A作AD⊥OB于D,
∵OA=OB=2,∠AOB=45°,
∴AD=OD=2×
=
,
∴点A(
,
),B(2,0),
∵C是AB中点,
∴点C的坐标为(
,
),
∴点O关于点C的对称点的坐标是(2+
,
).
故答案为:(2+
,
).
 解:如图,过点A作AD⊥OB于D,
解:如图,过点A作AD⊥OB于D,∵OA=OB=2,∠AOB=45°,
∴AD=OD=2×
| ||
| 2 |
| 2 |
∴点A(
| 2 |
| 2 |
∵C是AB中点,
∴点C的坐标为(
2+
| ||
| 2 |
| ||
| 2 |
∴点O关于点C的对称点的坐标是(2+
| 2 |
| 2 |
故答案为:(2+
| 2 |
| 2 |
点评:本题考查了坐标与图形变化-旋转,等腰直角三角形的性质,中点公式,比较简单,熟记公式并作出辅助线是解题的关键.

练习册系列答案
相关题目
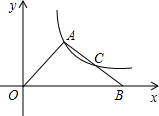 (2012•泸州)如图,在△OAB中,C是AB的中点,反比例函数y=
(2012•泸州)如图,在△OAB中,C是AB的中点,反比例函数y=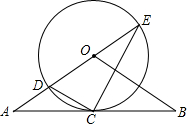 如图,在△OAB中,OA=OB,以点O为圆心的⊙0经过AB的中点C,直线AO与⊙0相交于点D、E,连接CD、CE.
如图,在△OAB中,OA=OB,以点O为圆心的⊙0经过AB的中点C,直线AO与⊙0相交于点D、E,连接CD、CE. 如图,在△OAB中,C是AB的中点,反比例函数y=
如图,在△OAB中,C是AB的中点,反比例函数y= 如图,在△OAB中,∠B=90°,∠BOA=30°,OA=4,将△OAB绕点O按逆时针方向旋转至△OA′B′,C点的坐标为(0,4).
如图,在△OAB中,∠B=90°,∠BOA=30°,OA=4,将△OAB绕点O按逆时针方向旋转至△OA′B′,C点的坐标为(0,4).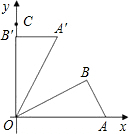 (创新学习)如图,在△OAB中,∠B=90°,∠BOA=30°,OA=4,将△OAB绕点O按逆时针方向旋转至△OA′B′,C点的坐标为(0,4).
(创新学习)如图,在△OAB中,∠B=90°,∠BOA=30°,OA=4,将△OAB绕点O按逆时针方向旋转至△OA′B′,C点的坐标为(0,4).