Question

7．三角形的三个内角分别为75°，80°，25°，现有一条直线将它分成两个等腰三角形，那么这两个等腰三角形的顶角的度数分别是130°、80°．

Answer 1

分析 首先在△ACB的内部做∠ACD=25°，从而可得到△ADC为等腰三角形，然后再证明△BDC为等腰三角形，从而可得到问题的答案．

解答 解：如图所示：∠A=25°，∠B=80°，∠ACB=75°．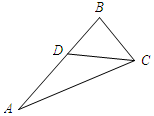

作∠ACD=∠A=25°，则三角形ADC为等腰三角形，且∠DCB=75°-25°=50°．
由三角形的外角的性质可知∠BDC=∠A+∠ACD=50°．
∴∠DCB=∠BDC，
∴△BDC为等腰三角形．
∴∠ADC=180°-50°=130°．
∴两个等腰三角形的顶角分别为130°、80°．
故答案为：130°、80°．

点评 本题主要考查的是等腰三角形的判定、三角形的外角的性质，熟练掌握相关知识是解题的关键．