题目内容
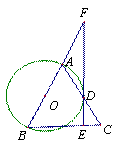
已知:如图,在直角△ABC中,∠ABC=90°,延长AB至点D,使AD=AC,取AC的中点为F,连DF交BC于点G,并延长至点E,使AE=CE.
(1)求证:⊿ABC≌⊿ADF;
(2)求证: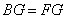 .(改编)
.(改编)
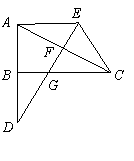 |
(1)证明:∵AE=CE,F为AC的中点,
∴EF⊥AC
∵∠ABC=90°,
∴∠ABC=∠AFE ∵AC=AE, ∠EAF=∠CAB,
∴⊿ABC≌⊿AFE
(2) ∴⊿ABC≌⊿AFE
 ∴AB=AF
∴AB=AF
连接AG,
∵AG=AC,AB=AF,
∴Rt⊿ABG≌Rt⊿AFG
BG=FG

练习册系列答案
相关题目
 )。
)。
 且AB>BC,那么下列最确切的结论是( ).
且AB>BC,那么下列最确切的结论是( ). D、AC=BC
D、AC=BC 解得情况是 .
解得情况是 .  (改编)
(改编)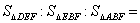 9: 21:49 ,则DE:EC= ( )
9: 21:49 ,则DE:EC= ( )
 B、-0.2 C、
B、-0.2 C、
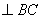 垂足为E,延长ED交BA的延长线于点F.
垂足为E,延长ED交BA的延长线于点F.