题目内容
13.在△ABC中,∠C=90°,AC=8,AB=10,以点C为圆心,以r=6为半径作圆,判断A、B两点和⊙C的位置关系.分析 根据题意画出图形,根据勾股定理求出BC的长,再由点与圆的位置关系即可得出结论.
解答  解:如图所示,
解:如图所示,
∵在△ABC中,∠C=90°,AC=8,AB=10,
∴BC=$\sqrt{{AB}^{2}-{AC}^{2}}$=$\sqrt{{10}^{2}-{8}^{2}}$=6,
∵AC>6,BC=6,
∴点A在圆外,点B在圆上.
点评 本题考查的是点与圆的位置关系,熟知点与圆的三种位置关系是解答此题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
1.若$\frac{x}{2y}$=$\frac{y}{x-y}$,则$\frac{{x}^{2}-2xy-3{y}^{2}}{{x}^{2}+4xy+3{y}^{2}}$=( )
| A. | 0 | B. | -$\frac{3}{2}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{3}{2}$或-$\frac{1}{5}$ |
5.$\sqrt{(-4)^{2}}$的平方根与$\sqrt{(-2)^{2}}$的和的绝对值是( )
| A. | 0 | B. | 4 | C. | 0或2 | D. | 4或0 |
2.若一元二次方程3x2-mx+8=0的一个根为2,则m的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 无法确定 |
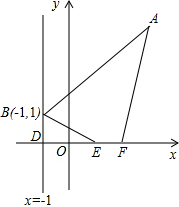 已知点A(3,4),点B(-1,1),在x轴上另取两点E,F(点E在点F的左侧),且EF=1,线段EF在x上平移,线段EF平移至何处时,四边形ABEF的周长最小?求出此时点E的坐标.
已知点A(3,4),点B(-1,1),在x轴上另取两点E,F(点E在点F的左侧),且EF=1,线段EF在x上平移,线段EF平移至何处时,四边形ABEF的周长最小?求出此时点E的坐标.