题目内容
如图,已知线段AB,分别以A、B为圆心,大于 AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC.那么:
AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC.那么:(1)∠ADC=______度;
(2)当线段AB=4,∠ACB=60°时,∠ACD=30度,△ABC的面积等于______

【答案】分析:利用线段垂直平分的性质,等腰三角形的性质和解直角三角形等知识点计算.
解答:解:(1)△ABC,△AQB中,AC=AQ,BC=BQ,AB=AB,△ABC≌△ABQ,∠CAB=∠QAB,
根据等腰三角形性质,我们可知:
AD是等腰△ACQ底边的高、中线和顶角的平分线.
∴∠ADC=90°.
(2)AC=AB,∠ACB=60°,
∴△ABC是等边三角形.
CD⊥AB,
∴∠ACD=∠BCD=30°.
CD=BC•sin60°=2 .
.
那么S△ABC=AB•CD÷2=4×2 ÷2=4
÷2=4 .
.
点评:本题综合考查了线段垂直平分的性质,等腰三角形的性质和解直角三角形等知识点,虽然知识点比较多,但只要找准确所求与已知的关系,本题并不难解.
解答:解:(1)△ABC,△AQB中,AC=AQ,BC=BQ,AB=AB,△ABC≌△ABQ,∠CAB=∠QAB,
根据等腰三角形性质,我们可知:
AD是等腰△ACQ底边的高、中线和顶角的平分线.
∴∠ADC=90°.
(2)AC=AB,∠ACB=60°,
∴△ABC是等边三角形.
CD⊥AB,
∴∠ACD=∠BCD=30°.
CD=BC•sin60°=2
 .
.那么S△ABC=AB•CD÷2=4×2
 ÷2=4
÷2=4 .
.点评:本题综合考查了线段垂直平分的性质,等腰三角形的性质和解直角三角形等知识点,虽然知识点比较多,但只要找准确所求与已知的关系,本题并不难解.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
如图,已知线段AB=10cm,点C是AB上任一点,点M、N分别是AC和CB的中点,则MN的长度为( )


| A、6cm | B、5cm | C、4cm | D、3cm |
 如图,已知线段AB,延长AB至C,使得BC=
如图,已知线段AB,延长AB至C,使得BC=| 1 |
| 2 |
| A、4cm | B、8cm |
| C、10cm | D、12cm |


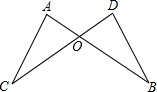 如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.
如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.