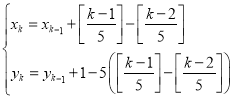Question

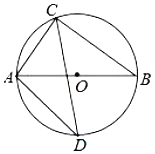
【题目】如图，已知AB是⊙O的直径，BC是⊙O的切线，连接AC与⊙O交于点 D．取BC的中点E，连接DE，并连接OE交⊙O于点F．连接AF交BC于点G，连接BD交AG于点H．

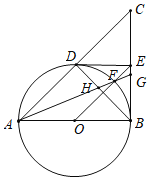
（1）若EF＝1，BE＝，求∠EOB的度数；

（2）求证：DE为⊙O的切线；

（3）求证：点F为线段HG的中点．

Answer 1

【答案】（1）∠EOB＝60°；（2）见解析；（3）见解析.

【解析】

（1）根据切线的性质得到∠ABC=90°，解直角三角形得到∠EOB=60°；
（2）连结OD，根据圆周角定理得到∠ADB=∠BDC=90°，求得DE=EC，根据切线的判定定理即可得到结论；
（3）根据三角形的中位线的性质得到OE∥AC，根据平行线的性质得到OE⊥BD，得到，求得∠FBD=∠FAB，根据等腰三角形的性质即可得到结论．

（1）∵AB是⊙O的直径，BC是⊙O的切线，

∴∠ABC＝90°，

在直角三角形OBE中，设圆O半径为r，

∵EF＝1，BE＝，则，r2+（）2＝（r+1）2，

解得r＝1，

∴OB＝1，OE＝2，

在Rt△OBE中，cos∠EOB＝,

∴∠EOB＝60°；

（2）连结OD，

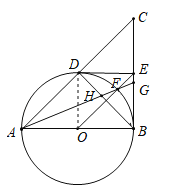
∵AB是⊙O的直径，

∴∠ADB＝∠BDC＝90°，

∵E为直角三角形BCD斜边的中点，

∴DE＝EC，

∴∠CDE＝∠C，

∵OD＝OA，

∴∠OAD＝∠ODA，

∴∠ODA+∠CDE＝∠OAD+∠C＝90°，

∴∠ODE＝180°﹣90°＝90°，

∴DE是⊙O的切线；

（3）连接BF，

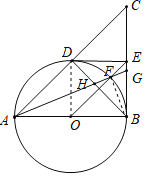
∵AB是圆O的直径，

∴∠AFB=90°，即BF⊥AF，

∵O、E分别为AB、BC的中点，

∴OE∥AC，

∵BD⊥AC，

∴OE⊥BD，

∴，

∴∠DOF=

∵∠BAF=

∴∠BAF=∠DOF,

∵∠DOF=∠DBF，

∴∠DBF=∠BAF，

∵BC是⊙O的切线，

∴∠EBF+∠ABF=90°

∵∠BAF+∠ABF=90°

∴∠EBF=∠BAF

∴∠EBF=∠HBF

∵BF⊥HG，

∴BF垂直平分HG，

即：点F为线段HG的中点．