题目内容
已知α为锐角，则关于x的方程x3-x2+（sinα-3）x+1=0的根的情况是（ ）
| A、只有一个正根 |
| B、有三个正根 |
| C、有一个正根，两个负根 |
| D、有两个正根，一个负根 |
考点：一元二次方程根的分布
专题：
分析：由于α为锐角，故可用特殊值法取α=30°，再判断出方程根的情况即可．
解答：解：取α=30°，原方程变为x3-x2-
x+1=0，即2x3-2x2-5x+2=0，
2x3-4x2+（2x2-5x+2）=0，
故（x-2）（2x2+2x-1）=0，
∴方程有两个正根，一个负根．
故选D．
| 5 |
| 2 |
2x3-4x2+（2x2-5x+2）=0，
故（x-2）（2x2+2x-1）=0，
∴方程有两个正根，一个负根．
故选D．
点评：本题考查的是一元二次方程根的分布，熟知特殊值法是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
下列各数的值为负数的是（ ）
| A、0×（-1） |
| B、（-1）×（-2）×（-3） |
| C、（-7）×（-2） |
| D、（-4）×（-2）2×（-10） |
已知|a|=3，|b|=
，且a＜0＜b，则a，b的值分别为（ ）
| 1 |
| 3 |
A、3，
| ||
B、-3，
| ||
C、-3，-
| ||
D、3，-
|
人的正常体温约是37℃，我们把体温超过正常体温的部分记作正数，那么-0.2℃表示（ ）
| A、体温为零下0.2℃ |
| B、体温为零上0.2℃ |
| C、体温为37.2℃ |
| D、体温为36.8℃ |
下列方程中是关于x的一元二次方程的是（ ）
| A、ax2+bx+c=0 | ||
| B、（x-1）（x+2）=1 | ||
C、x2+
| ||
| D、3x2-2xy-5y2=0 |
下列方程中，关于x的一元二次方程是（ ）
A、
| ||||
| B、3（x+1）2=2（x+1） | ||||
C、
| ||||
| D、2x2-3xy+y2=9 |
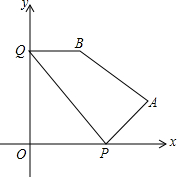如图，在平面直角坐标系中，A点的坐标是（12，3），B点的坐标是（2，7），在x，y轴上分别有一点P和Q，若有四边形PABQ的周长最短，求周长最短的值．
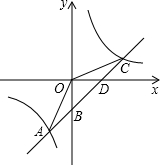如图，一次函数y=kx+b的图象与反比例函数y=