题目内容
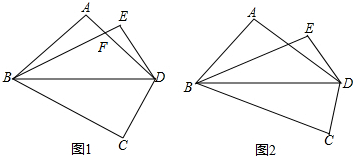
15.已知:如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,连结对角线BD,将△BCD沿BD翻折,使点E与点C对称,BE交AD于点F.(1)如图1,求证:∠ABF=∠EDF;
(2)如图2,当∠CBD=22.5°时,请找出BF与CD的数量关系,并说明理由.
分析 (1)由已知条件得到∠ABF+∠FBD=45°,根据∠FDB+∠FBD+∠FDE=90°,∠FDB=45°,于是得到∠FBD+∠FDE=45°,即可得到结论;
(2)延长DC到G使CD=CG,连接BG,于是得到∠CBG=∠CBD=22.5°,求得∠GBA=90°,证得四边形BGDF是梯形,求出∠G=∠FBG,得到四边形BGDF是等腰梯形,于是得到结论.
解答 (1)证明:∵∠A=∠C=90°,AB=AD,
∴∠ABF+∠FBD=45°,
∵∠FDB+∠FBD+∠FDE=90°,∠FDB=45°,
∴∠FBD+∠FDE=45°,
∴∠ABF=∠FDE;
(2)解:延长DC到G使CD=CG,连接BG,
∴∠CBG=∠CBD=22.5°,
∴∠GBA=90°,
∴四边形BGDF是梯形,∠G=90°-∠CBG=67.5°,∠FBG=∠FBD+∠DBC+∠CBG=67.5°,
∴四边形BGDF是等腰梯形,
∴BF=DG=2CD.
点评 本题考查了翻折变换-折叠问题,等腰直角三角形的性质,等腰梯形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
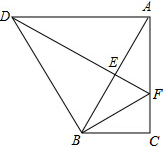 如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.
如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF. 如图,长方形ABCD的长是a,宽是b,分别以A,B为圆心,b为半径作圆,交AB于点E,F,列式表示阴影部分的周长l和面积S.
如图,长方形ABCD的长是a,宽是b,分别以A,B为圆心,b为半径作圆,交AB于点E,F,列式表示阴影部分的周长l和面积S.