题目内容
4.如图,每一幅图中均含有若干个正方形,第1幅图中有1个正方形;第2幅图中有5个正方形;按这样的规律下去,第4幅图中有( )个正方形.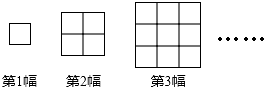
| A. | 30 | B. | 31 | C. | 32 | D. | 33 |
分析 观察图形发现:第1幅图中有1个正方形,第2幅图中有1+4=5个正方形,第3幅图中有1+4+9=14个正方形,…由此得出第n幅图中有12+22+32+42+…+n2=$\frac{1}{6}$n(n+1)(2n+1)从而得到答案.
解答 解:∵第1幅图中有1个正方形,
第2幅图中有1+4=5个正方形,
第3幅图中有1+4+9=14个正方形,
…
∴第n幅图中有12+22+32+42+…+n2=$\frac{1}{6}$n(n+1)(2n+1),
∴第4幅图中有12+22+32+42=30个正方形.
故选:A.
点评 此题考查图形的变化规律,利用图形之间的联系,得出数字的运算规律解决问题.

练习册系列答案
相关题目
12.已知等腰三角形底边长和腰长是方程x2-9x+18=0的两根,则这个等腰三角形的周长为( )
| A. | 15 | B. | 12 | C. | 15或12 | D. | 18 |
16.某一动物细胞,细胞核与细胞壁之间的距离为0.0000075cm,用科学记数法表示为( )
| A. | 7.5×106cm | B. | 7.5×10-6cm | C. | 7.5×10-5cm | D. | -7.5×106cm |
13.一个数大于6,另一个数比10的相反数大2,则这两个数的和不可能是( )
| A. | 18 | B. | -1 | C. | -18 | D. | 2 |
14.下列每组中的两个代数式,属于同类项的是( )
| A. | $\frac{1}{2}$x2y与$\frac{2}{3}$xy2 | B. | $\frac{1}{2}$m3n与-8nm3 | C. | 3abc与3ab | D. | 0.5a2b与0.5a2c |
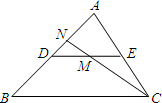 如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△DEA=1:6.
如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△DEA=1:6.