题目内容
如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:AE=DF.
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
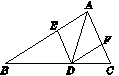
第21题图
.解:(1)证明:因为DE∥AC,DF∥AB,
所以四边形AEDF是平行四边形,
所以AE=DF.
(2)解:若AD平分∠BAC,则四边形AEDF是菱形,理由如下:
因为DE∥AC,DF∥AB,
所以四边形AEDF是平行四边形,且∠BAD=∠FDA.
又AD平分∠BAC,所以∠BAD=∠DAF,
所以∠DAF=∠FDA,
所以AF=DF,
所以平行四边形AEDF为菱形.

练习册系列答案
相关题目
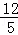 ,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D
,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D ,使四边形ABCD为对等四边形,并求出CD的长.
,使四边形ABCD为对等四边形,并求出CD的长.
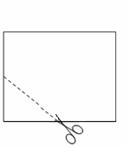
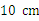 ,宽为
,宽为 的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( ) B.
B. C.
C.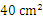 D.
D.
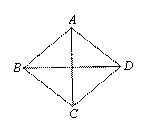
 ,一条对角线长为
,一条对角线长为 ,则这个菱形的面积为_________.
,则这个菱形的面积为_________. 中,∠
中,∠ ,
,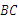 的垂直平分线
的垂直平分线 交
交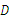 ,交
,交 于点
于点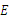 ,点
,点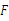 在
在 .
. 是平行四边形.
是平行四边形. 满足什么条件时,四边形
满足什么条件时,四边形

 …………………………( )
…………………………( )
 ,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率. 米,则扇形OAB的面积为
米,则扇形OAB的面积为 平方米 B.
平方米 B.  平方米
平方米  平方米 D.
平方米 D.  平方米
平方米