题目内容
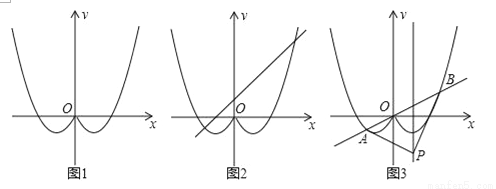
如图,将函数y=x2﹣2x(x≥0)的图象沿y轴翻折得到一个新的图象,前后两个图象其实就是函数y=x2﹣2|x|的图象.
(1)观察思考
函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;方程x2﹣2|x|=2有 个实数根;关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 ;
(2)拓展探究
①如图2,将直线y=x+1向下平移b个单位,与y=x2﹣2|x|的图象有三个交点,求b的值;
②如图3,将直线y=kx(k>0)绕着原点旋转,与y=x2﹣2|x|的图象交于A、B两点(A左B右),直线x=1上有一点P,在直线y=kx(k>0)旋转的过程中,是否存在某一时刻,△PAB是一个以AB为斜边的等腰直角三角形(点P、A、B按顺时针方向排列).若存在,请求出k值;若不存在,请说明理由.
练习册系列答案
相关题目


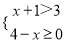 的解集用数轴表示为( )
的解集用数轴表示为( )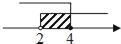 B.
B. 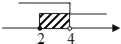
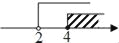 D.
D. 
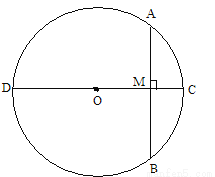
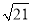 cm
cm