题目内容
14.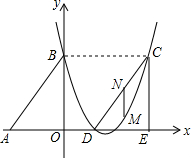 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}{x}^{2}+bx+c$经过B点,且顶点在直线x=$\frac{5}{2}$上.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}{x}^{2}+bx+c$经过B点,且顶点在直线x=$\frac{5}{2}$上.(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l,当l取最大值时,是否在x轴上存在一点F,在y轴上存在一点G,使四边形MFGN的周长最小?若存在,请求出点F、点G的坐标,并求出这个四边形周长的最小值;若不存在,请说明理由.
分析 (1)已知了抛物线上A、B点的坐标以及抛物线的对称轴方程,可用待定系数法求出抛物线的解析式.
(2)首先求出AB的长,将A、B的坐标向右平移AB个单位,即可得出C、D的坐标,再代入抛物线的解析式中进行验证即可.
(3)根据C、D的坐标,易求得直线CD的解析式;那么线段MN的长实际是直线BC与抛物线的函数值的差,可将x=t代入两个函数的解析式中,得出的两函数值的差即为l的表达式,由此可求出l、t的函数关系式,根据所得函数的性质即可求出l取最大值时,点M、点N的坐标;作M关于x轴的对称点M′,作N关于y轴的对称点N′,连结M′N′分别交x轴,y轴于F,G,则MF+FG+GN的总路径最短,由题意可得:M′的坐标为($\frac{7}{2},-\frac{1}{2}$),N′的坐标为(-$\frac{7}{2}$,2),求得M′N′的解析式为:$y=-\frac{5}{14}+\frac{3}{4}$,从而得F的坐标为($\frac{21}{10}$,0),G的坐标为(0,$\frac{3}{4}$),所以可以求得四边形MFGN的最小值为:MF+FG+GN+MN=M′N′+MN=$\frac{\sqrt{221}}{2}+\frac{3}{2}$.
解答 解:(1)∵抛物线y=$\frac{2}{3}{x}^{2}+bx+c$顶点在直线x=$\frac{5}{2}$上
∴可设所求抛物线对应的函数关系式为y=$\frac{2}{3}(x-\frac{5}{2})^{2}$+m
∵点B(0,4)在此抛物线上,
∴4=$\frac{2}{3}×(-\frac{5}{5})^{2}$+m
∴m=-$\frac{1}{6}$
∴所求函数关系式为:y=$\frac{2}{3}(x-\frac{5}{2})^{2}-\frac{1}{6}=\frac{2}{3}{x}^{2}-\frac{10}{3}x$+4.
(2)在Rt△ABO中,OA=3,OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5
∵四边形ABCD是菱形
∴BC=CD=DA=AB=5
∴C、D两点的坐标分别是(5,4)、(2,0);
当x=5时,y=$\frac{2}{3}×{5}^{2}-\frac{10}{3}×5+4$=4,
当x=2时,y=$\frac{2}{3}×{2}^{2}-\frac{10}{3}×2+$4=0,
∴点C和点D在所求抛物线上;
(3)设直线CD对应的函数关系式为y=kx+b,
根据题意,得$\left\{\begin{array}{l}{5k+b=4}\\{2k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{8}{3}}\end{array}\right.$
∴y=$\frac{4}{3}x-\frac{8}{3}$,
∵MN平行于y轴交CD于点N.设点M的横坐标为t,
∴N点的横坐标也为t,
则${y}_{M}=\frac{2}{3}{t}^{2}-\frac{10}{3}t+4$,${y}_{N}=\frac{4}{3}t-\frac{8}{3}$,
∴l=yM-yN=$\frac{4}{3}t-\frac{8}{3}-(\frac{2}{3}{t}^{2}-\frac{10}{3}t+4)$=-$\frac{2}{3}{t}^{2}+\frac{14}{3}t-\frac{20}{3}$=-$\frac{2}{3}(t-\frac{7}{2})^{2}+\frac{3}{2}$,
∵-$\frac{2}{3}<0$,
∴当t=$\frac{7}{2}$时,${l}_{最大}=\frac{3}{2}$,此时点M的坐标为($\frac{7}{2}$,$\frac{1}{2}$),点N的坐标为($\frac{7}{2}$,2),
如图,作M关于x轴的对称点M′,作N关于y轴的对称点N′,连结M′N′分别交x轴,y轴于F,G,
则MF+FG+GN的总路径最短,
由题意可得:M′的坐标为($\frac{7}{2},-\frac{1}{2}$),N′的坐标为(-$\frac{7}{2}$,2),
求得M′N′的解析式为:$y=-\frac{5}{14}x+\frac{3}{4}$,
得F的坐标为($\frac{21}{10}$,0),G的坐标为(0,$\frac{3}{4}$),
可以求得四边形MFGN的最小值为:MF+FG+GN+MN=M′N′+MN=$\frac{\sqrt{221}}{2}+\frac{3}{2}$.
点评 此题考查了二次函数综合题,其中涉及到的知识点有:待定系数法求一次函数、二次函数的解析式,函数图象上点的坐标特征,菱形的性质,图象的平移变换,二次函数的应用等知识.在(3)中利用二次函数的最值求出点M、点N的坐标;作M关于x轴的对称点M′,作N关于y轴的对称点N′,连结M′N′分别交x轴,y轴于F,G是解决本题的关键.

下表是从七年级学生中选出10名学生统计出的各自家庭一个月的节水情况:
| 节水量/m3 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| 家庭数/个 | 1 | 2 | 4 | 2 | 1 |
| A. | 0.4和0.3 | B. | 0.4和0.34 | C. | 0.4和0.4 | D. | 0.4和0.42 |
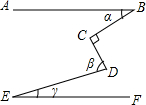 如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )| A. | ∠β=∠α+∠γ | B. | ∠α+∠β+∠γ=180° | C. | ∠α+∠β-∠γ=90° | D. | ∠β+∠γ-∠α=90° |
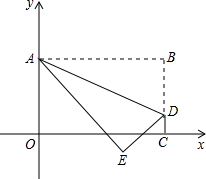 将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.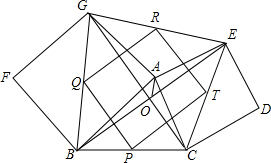 如图,已知△ABC,分别以AB,AC为边作正方形ABFG和正方形ACDE,连接BE,CG交于点O,联结AO,P、Q、R、T分别是BC、BG、EG、CE的中点.
如图,已知△ABC,分别以AB,AC为边作正方形ABFG和正方形ACDE,连接BE,CG交于点O,联结AO,P、Q、R、T分别是BC、BG、EG、CE的中点.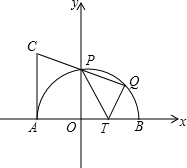 如图,在平面直角坐标系中,半径为2的半圆O与x轴交于A、B两点,与y轴交于点P,T是OB上的一点,OT=a(0<a<2),过A作AC⊥AB,且AC=AT,连接CP并延长交半圆于另一点Q,且Q恰为弧PB中点.
如图,在平面直角坐标系中,半径为2的半圆O与x轴交于A、B两点,与y轴交于点P,T是OB上的一点,OT=a(0<a<2),过A作AC⊥AB,且AC=AT,连接CP并延长交半圆于另一点Q,且Q恰为弧PB中点.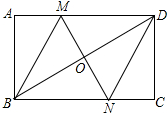 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.