题目内容
2．已知x、y满足方程组$\left\{\begin{array}{l}{2x+y=5}\\{x+2y=4}\end{array}\right.$，则y-x的值是-1．分析 方程组两方程相减即可求出y-x的值．
解答 解：$\left\{\begin{array}{l}{2x+y=5①}\\{x+2y=4②}\end{array}\right.$，
②-①得：y-x=-1．
故答案为：-1．
点评 此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
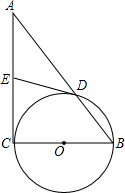如图，在Rt△ABC中，∠ACB=90°，以BC为直径作⊙O，交AB于点D，取AC的中点E，连接DE．
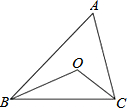如图，在△ABC中，BO、CO分别是∠ABC、∠ACB的角平分线，求：
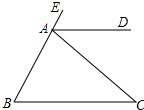如图，E、A、B三点在同一直线上，AD平分∠EAC，AD∥BC，∠B=50°，则∠C的度数50°．
如图，将一张长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置上，ED′的延长线与BC的交点为G，若∠EFG=56°，则∠2-∠1=44°．
14．在?ABCD中，∠A：∠B：∠C：∠D的值可能是（ ）
| A． | 3：4：3：4 | B． | 5：2：2：5 | C． | 2：3：4：5 | D． | 3：3：4：4 |
11．
如图，将周长为10的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为（ ）
如图，将周长为10的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为（ ）| A． | 8 | B． | 10 | C． | 12 | D． | 14 |