题目内容
 如图,⊙O是△ABC的外接圆,过点A、B两点分别作⊙O的切线PA、PB交于一点P,连接OP
如图,⊙O是△ABC的外接圆,过点A、B两点分别作⊙O的切线PA、PB交于一点P,连接OP(1)求证:∠APO=∠BPO;
(2)若∠C=60°,AB=6,点Q是⊙O上的一动点,求PQ的最大值.
考点:切线的性质
专题:
分析:(1)根据切线的性质得出OA⊥PA,OB⊥PB,然后根据HL证得RT△PAO≌RT△PBO,即可证得结论.
(2)根据切线的性质得出∠PAB=∠PBA=∠C=60°,OP⊥AB,从而证得△PAB为等边三角形,延长PO交⊙O于Q,连接AQ、BQ,则此时PQ最大,然后通过解直角三角形即可求得PQ的最大值.
(2)根据切线的性质得出∠PAB=∠PBA=∠C=60°,OP⊥AB,从而证得△PAB为等边三角形,延长PO交⊙O于Q,连接AQ、BQ,则此时PQ最大,然后通过解直角三角形即可求得PQ的最大值.
解答: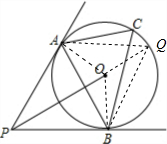 (1)证明:连接OA、OB,
(1)证明:连接OA、OB,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
在RT△PAO和RT△PBO中,
,
∴RT△PAO≌RT△PBO(HL),
∴∠APO=∠BPO;
(2)解:∵PA、PB是⊙O的切线,
∴∠PAB=∠PBA=∠C=60°,OP⊥AB,
∴△PAB为等边三角形,
延长PO交⊙O于Q,连接AQ、BQ,则此时PQ最大,
∵∠APB=60°,
∴∠APO=∠BPO=30°
∴PQ=2×
AP=2×
AB=2×
×6=6
.
 (1)证明:连接OA、OB,
(1)证明:连接OA、OB,∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
在RT△PAO和RT△PBO中,
|
∴RT△PAO≌RT△PBO(HL),
∴∠APO=∠BPO;
(2)解:∵PA、PB是⊙O的切线,
∴∠PAB=∠PBA=∠C=60°,OP⊥AB,
∴△PAB为等边三角形,
延长PO交⊙O于Q,连接AQ、BQ,则此时PQ最大,
∵∠APB=60°,
∴∠APO=∠BPO=30°
∴PQ=2×
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
点评:本题考查了切线的性质,等边三角形的判定,直角三角函数的应用,连接OA、OB是常用的辅助线的方法.

练习册系列答案
相关题目
在1,
,
,
,
,0.3131131113…中,无理数共有( )
| 22 |
| 7 |
| 3 |
| 3 | 27 |
| π |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,
如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°, 已知如图,△ABC是等腰直角三角形,∠BAC=90°,将△ABP绕点A逆时针方向转动到△ACP′,若AP=3cm,AB=4cm,求BC、PP′的长.
已知如图,△ABC是等腰直角三角形,∠BAC=90°,将△ABP绕点A逆时针方向转动到△ACP′,若AP=3cm,AB=4cm,求BC、PP′的长. 如图,AB是半⊙的直径,AC为弦,D为
如图,AB是半⊙的直径,AC为弦,D为
 如图,在Rt△ABC中,∠BAC=90°,如果将该三角形绕点A按顺时针方向旋转到△AB′C′的位置,点B′恰好落在边BC的中点处,求旋转角的大小.
如图,在Rt△ABC中,∠BAC=90°,如果将该三角形绕点A按顺时针方向旋转到△AB′C′的位置,点B′恰好落在边BC的中点处,求旋转角的大小. 如图,长方形纸片ABCD中,已知AD=8,AB=6,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,则CE的长为
如图,长方形纸片ABCD中,已知AD=8,AB=6,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,则CE的长为