题目内容
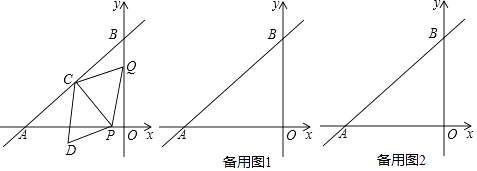
【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是 .
(k<0)上运动,则k的值是 . 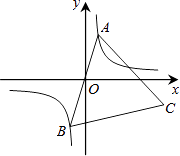
【答案】﹣3
【解析】解:∵双曲线y= ![]() 关于原点对称, ∴点A与点B关于原点对称.
关于原点对称, ∴点A与点B关于原点对称.
∴OA=OB.
连接OC,如图所示.
∵△ABC是等边三角形,OA=OB,
∴OC⊥AB.∠BAC=60°.
∴tan∠OAC= ![]() =
= ![]() .
.
∴OC= ![]() OA.
OA.
过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,
∵AE⊥OE,CF⊥OF,OC⊥OA,
∴∠AEO=∠OFC,∠AOE=90°﹣∠FOC=∠OCF.
∴△AEO∽△OFC.
∴ ![]() =
= ![]() =
= ![]() .
.
∵OC= ![]() OA,
OA,
∴OF= ![]() AE,FC=
AE,FC= ![]() EO.
EO.
设点A坐标为(a,b),
∵点A在第一象限,
∴AE=a,OE=b.
∴OF= ![]() AE=
AE= ![]() a,FC=
a,FC= ![]() EO=
EO= ![]() b.
b.
∵点A在双曲线y= ![]() 上,
上,
∴ab=1.
∴FCOF= ![]() b
b ![]() a=3ab=3,
a=3ab=3,
设点C坐标为(x,y),
∵点C在第四象限,
∴FC=x,OF=﹣y.
∴FCOF=x(﹣y)=﹣xy=3.
∴xy=﹣3.
∵点C在双曲线y= ![]() 上,
上,
∴k=xy=﹣3.
所以答案是:﹣3.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

练习册系列答案
相关题目