��Ŀ����
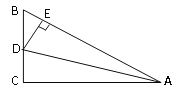
����Ŀ����ͼ���ھ���ABCD�У�AB=6��BC=8������Q�ӵ�A����������AB������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�B���������ŶԽ���BD����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5������PΪԲ�ģ�PB��Ϊ�뾶�ġ�P��BD��AB����һ������ֱ�ΪE��F������EF��QE�� 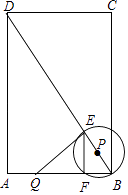
��1����գ�FB=����t�Ĵ���ʽ��ʾ����
��2����tΪ��ֵʱ����Q���F������
��3�����߶�QE���P������������ʱ����t��ȡֵ��Χ��
���𰸡�
��1��![]() t
t
��2���⣺����Q���F����ʱ��AQ+BF=AB��
��t+ ![]() t=6��
t=6��
��t= ![]() s��
s��
�൱t= ![]() sʱ����Q���F����
sʱ����Q���F����
��3���⣺��ֱ��QE���P����ʱ��
�ߡ�BEQ=��A=90�㣬��QBE=��ABD��
���QBE�ס�DBA��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��t= ![]() s��
s��
���߶�QE���P�����������㣬
��t��ȡֵ��Χ�� ![]() ��t��
��t�� ![]() ��
��
���������⣺��1����BE�ǡ�P��ֱ�����ı���ABCD�Ǿ��Σ� ���EFB=��A=90��
��Rt��ABC����AD=8��AB=6��
��BD= ![]() =10��
=10��
��EF��AD��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��BF= ![]() t��
t��
����Ϊ ![]() t��
t��

��ϰ��ϵ�д�
�����Ŀ