题目内容
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(﹣4,0),B(0,3),动点P从点O出发,沿x轴负方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造平行四边形PQCD,设点P运动的时间为t秒. 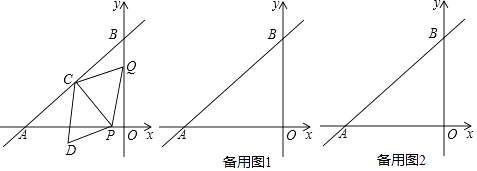
(1)当点Q在线段OB上时,用含t的代数式表示PC,AC的长;
(2)在运动过程中. ①当点D落在x轴上时,求出满足条件的t的值;
②若点D落在△ABO内部(不包括边界)时,直接写出t的取值范围;
(3)作点Q关于x轴的对称点Q′,连接CQ′,在运动过程中,是否存在某时刻使过A,P,C三点的圆与△CQQ′三边中的一条边相切?若存在,请求出t的值;若不存在,请说明理由.#D.
【答案】
(1)解:如图1中,
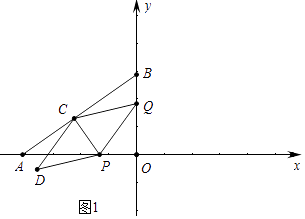
∵OA=3,OB=4,
∴AB= ![]() =
= ![]() =5,
=5,
在Rt△ACP中,PA=4﹣t,
∵sin∠OAB= ![]() =
= ![]() ,
,
∴PC= ![]() (4﹣t),
(4﹣t),
∵cos∠OAB= ![]() =
= ![]() ,
,
∴AC= ![]() (4﹣t)
(4﹣t)
(2)解:①当D在x轴上时,如图2中,

∵QC∥OA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() .
.
∴t= ![]() s时,点D在x轴上,
s时,点D在x轴上,
②如图,

∵PQ∥AB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() ,
,
综上所述,当 ![]() <t<
<t< ![]() 时,点D落在△ABO内部(不包括边界)
时,点D落在△ABO内部(不包括边界)
(3)解:如图3中,作QN⊥BC于N,
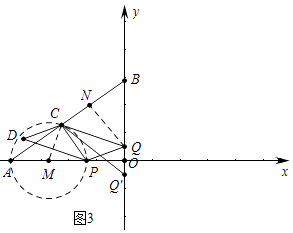
∵Q(0,3﹣2t),Q′(0,2t﹣3),
当QC与⊙M相切时,则QC⊥CM,
∴∠QCM=90°,∴∠QCP+∠PCM=90°,∵∠QCP+∠QCB=90°,
∴∠BCQ=∠PCM=∠CPM,
∵∠CPM+∠PAC=90°,∠OBA+∠OAB=90°,
∴∠APC=∠OBA,∴∠QBC=∠QCB,
∴BQ=CQ,
∵cos∠ABO= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() ,
,
当CQ′是⊙M切线时,同法可得 ![]() =
= ![]() ,
,
解得t= ![]() ,
,
∴t= ![]() s或
s或 ![]() 时,过A,P,C三点的圆与△CQQ′三边中的一条边相切
时,过A,P,C三点的圆与△CQQ′三边中的一条边相切
【解析】(1)利用三角函数sin∠OAB= ![]() =
= ![]() ,cos∠OAB=
,cos∠OAB= ![]() =
= ![]() ,列出关系式即可解决问题.(2)①当D在x轴上时,如图2中,由QC∥OA,得
,列出关系式即可解决问题.(2)①当D在x轴上时,如图2中,由QC∥OA,得 ![]() =
= ![]() ,由此即可解决问题.②当点D在AB上时,如图3中,由PQ∥AB,得
,由此即可解决问题.②当点D在AB上时,如图3中,由PQ∥AB,得 ![]() =
= ![]() ,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.(3)如图4中,当QC与⊙M相切时,则QC⊥CM,首先证明QB=QC,作QN∠BC于N,根据cos∠ABO=
,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.(3)如图4中,当QC与⊙M相切时,则QC⊥CM,首先证明QB=QC,作QN∠BC于N,根据cos∠ABO= ![]() =
= ![]() ,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似.
,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似.

 智能训练练测考系列答案
智能训练练测考系列答案