题目内容
已知关于x的方程x2+2(a-1)x+a2-7a-7=0的两个根为x1,x2,且满足x1x2-3x1-3x2-2=0,求(1+
)•
的值.
| 4 |
| a2-4 |
| a+2 |
| a |
考点:根与系数的关系,分式的化简求值,根的判别式
专题:
分析:先根据根与系数的关系用a表示出x1+x2,及x1•x2的值,再代入方程x1x2-3x1-3x2-2=0中求出a的值,把所求分式进行化简,把a的值代入即可.
解答:解:∵关于x的方程x2+2(a-1)x+a2-7a-4=0的两根为x1、x2,
∴当4(a-1)2-4(a2-7a-4)≥0,即a≥-1时,方程有解,
x1+x2=-2(a-1),x1•x2=a2-7a-4,
∵x1x2-3x1-3x2-2=0,
∴a2-7a-4+6(a-1)-2=0,解得a=-3或a=4,
∵a≥-1时,方程有解,
∴a=-3不合题意,
∴a=4,
∵(1+
)•
=
•
=
,
∴当a=4时,原式=2.
∴当4(a-1)2-4(a2-7a-4)≥0,即a≥-1时,方程有解,
x1+x2=-2(a-1),x1•x2=a2-7a-4,
∵x1x2-3x1-3x2-2=0,
∴a2-7a-4+6(a-1)-2=0,解得a=-3或a=4,
∵a≥-1时,方程有解,
∴a=-3不合题意,
∴a=4,
∵(1+
| 4 |
| a2-4 |
| a+2 |
| a |
=
| a2 |
| a2-4 |
| a+2 |
| a |
=
| a |
| a-2 |
∴当a=4时,原式=2.
点评:本题考查的是根与系数的关系及分式的化简求值,先根据根与系数的关系求出a的值是解答此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
在下列各组图形中,是全等的图形是( )
A、 |
B、 |
C、 |
D、 |
如果有理数x、y满足|x-1|+(y+3)2=0,则(xy)2的值是( )
| A、6 | B、-6 | C、9 | D、-9 |
下列各组中的两项是同类项的是( )
| A、0.5a和0.5b | ||
| B、-m2n和-mn2 | ||
| C、-m2和3m | ||
D、8xy2和-
|
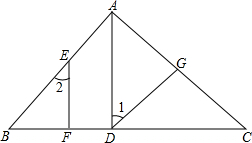 如图,在△ABC中,AD⊥BC于点D,EF⊥BC于点F,∠B=∠GDC,试说明∠1=∠2的理由.
如图,在△ABC中,AD⊥BC于点D,EF⊥BC于点F,∠B=∠GDC,试说明∠1=∠2的理由.