题目内容
 为调动学生学习积极性,某中学初一(1)班对学生的学习表现实行每月评分制,现对初一上期1-5学月的评分情况进行统计,其中学生小明5次得分情况如下表所示:
为调动学生学习积极性,某中学初一(1)班对学生的学习表现实行每月评分制,现对初一上期1-5学月的评分情况进行统计,其中学生小明5次得分情况如下表所示:| 时间 | 第1学月 | 第2学月 | 第3学月 | 第4学月 | 第5学月 |
| 得分 | 8分 | 9分 | 9分 | 9分 | 10分 |
(1)若小明和小刚这5次得分的平均成绩相等,求出小刚第3学月的得分;
(2)在图中直接补全折线统计图;
(3)据统计,小明和小刚这5学月的总成绩都排在了班级的前4名,现准备从该班的前四名中任选两名同学参加学校的表彰大会,请用列表或画树状图的方法,求选取的两名同学恰好是小明和小刚两人的概率.
考点:折线统计图,列表法与树状图法
专题:
分析:(1)根据表中的数据先求出小明的平均成绩,再根据小明和小刚这5次得分的平均成绩相等,求出小刚的总得分,再减去1月份、2月份、4月份、5月份的得分,即可得出第3学月的得分;
(2)根据小刚的3月份的得分,即可补全折线统计图;
(3)先用A表示小明,用B表示小刚,C、D分别表示剩下的两名同学,画出树状图,根据概率公式即可求出选取的两名同学恰好是小明和小刚两人的概率.
(2)根据小刚的3月份的得分,即可补全折线统计图;
(3)先用A表示小明,用B表示小刚,C、D分别表示剩下的两名同学,画出树状图,根据概率公式即可求出选取的两名同学恰好是小明和小刚两人的概率.
解答:解:(1)小明的平均成绩是:(8+9+9+9+10)÷5=9(分),
∵小明和小刚这5次得分的平均成绩相等,
∴小刚的平均成绩是9分,
∴小刚第3学月的得分是5×9-8-10-9-8=10(分);
(2)小刚第3学月的得分是10分,补图如下:

(3)用A表示小明,用B表示小刚,C、D分别表示剩下的两名同学,列树状图如下:

共有12种情况,两名同学恰好是小明和小刚两人的概率是
=
.
∵小明和小刚这5次得分的平均成绩相等,
∴小刚的平均成绩是9分,
∴小刚第3学月的得分是5×9-8-10-9-8=10(分);
(2)小刚第3学月的得分是10分,补图如下:

(3)用A表示小明,用B表示小刚,C、D分别表示剩下的两名同学,列树状图如下:

共有12种情况,两名同学恰好是小明和小刚两人的概率是
| 2 |
| 12 |
| 1 |
| 6 |
点评:此题考查了折线统计图和列树状图求概率,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,折线统计图表示的是事物的变化情况,概率=所求情况数与总情况数之比.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
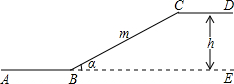 如图是某商场一楼与二楼之间的手扶电梯示意,其中AB、CD分别表示一楼、二楼地面的水平线,已知∠CBE=α,BC的长是m,则乘电梯从点B到点C上升的高度h为( )
如图是某商场一楼与二楼之间的手扶电梯示意,其中AB、CD分别表示一楼、二楼地面的水平线,已知∠CBE=α,BC的长是m,则乘电梯从点B到点C上升的高度h为( )| A、m•sinα | ||
B、
| ||
| C、m•cosα | ||
D、
|
 如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,AB=12,AO=8,则OC长为( )
如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,AB=12,AO=8,则OC长为( )| A、5 | ||
| B、4 | ||
C、2
| ||
D、2
|
 如图,AB∥CD,∠A=70°,则∠COE=
如图,AB∥CD,∠A=70°,则∠COE=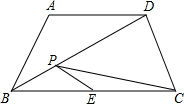 如图所示,在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,点P是对角线BD上的动点,则PE+PC的最小值是( )
如图所示,在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,点P是对角线BD上的动点,则PE+PC的最小值是( ) 小轿车从甲地出发驶往乙地,同时货车从相距乙地60km的入口处驶往甲地(两车均在甲、乙两地之间的公路上匀速行驶),如图是它们离甲地的路程y(km)与货车行驶时间x(h)之间的函数的部分图象.
小轿车从甲地出发驶往乙地,同时货车从相距乙地60km的入口处驶往甲地(两车均在甲、乙两地之间的公路上匀速行驶),如图是它们离甲地的路程y(km)与货车行驶时间x(h)之间的函数的部分图象.